
Ο πρόλογος του πλατωνικού διαλόγου Παρμενίδης παρέχει αρκετές από τις ελάχιστες, κατά τα άλλα, πληροφορίες που διαθέτουμε για τη ζωή του Ζήνωνα. Η πλειονότητα των μελετητών αποδέχεται τη δήλωση του Πλάτωνα σύμφωνα με την οποία, όταν ο Σωκράτης «ήταν πολύ νέος» [Σωκράτη δέ είναι τότε σφοδρά νέον (Παρμενίδης, 127
b)] και μολονότι αρκετά μεγάλος πια για να συμμετέχει σε φιλοσοφικές αντιπαραθέσεις, ο Ζήνωνας ήταν περίπου σαράντα ετών και ο Παρμενίδης εξήντα πέντε. Ο διάλογος διεξάγεται ενώ στην Αθήνα τελεί- ται η τετραετής γιορτή των Μεγάλων Παναθηναίων και ο πιο πιθανός δραματικός χρόνος που μπορούμε να εικάσουμε είναι το διάστημα μεταξύ του 454 π.Χ., όταν ο Σωκράτης είναι 15 ετών και του 450 π.Χ. όταν ο φιλόσοφος είναι 19 ετών. Προβάλλει, επίσης, εξαιρετικά πιθανή, αν και δεν επιβεβαιώνεται από άλλες πηγές, η μαρτυρία του Πλάτωνα (Παρμενίδης 127
b) ότι ο Ζήνωνας «ήταν ψηλός και ευπαρουσίαστος και φημολογούνταν ότι υπήρξε ερωμένος του Παρμενίδη» [
εὐμήκη δέ καί χαρίεντα ἰδεῖν καί λέγεσθαι αὐτόν παιδικά τοῦ Παρμενίδον γεγονέναΙ]. Ακόμη και αν από ιστορική άποψη η σκηνοθεσία του πλατωνικού Παρμενίδη κρίνεται ευλογοφανής, η κραυγαλέα έλλειψη αξιοπιστίας που χαρακτηρίζει τις αναφορές του Πλάτωνα στους πρώιμους φιλοσόφους επιβάλλει να σκεφτούμε ότι δεν είναι φρόνιμο να υιοθετούμε αβασάνιστα οποιαδήποτε δήλωσή του. Είναι βέβαιο ότι η συζήτηση των προσώπων του πλατωνικού Παρμενίδη δεν διεξήχθη ποτέ, και έχουμε κάθε λόγο να αμφιβάλουμε αν ο Σωκράτης συνάντησε ποτέ τους φιλοσόφους από την Ελέα. Επιπλέον, ο Πλάτωνας επισημαίνει ότι η πραγματεία του Ζήνωνα παρέμενε άγνωστη στην Αθήνα πριν από τον δραματικό χρόνο του Παρμενίδη (127
c)· υπονοεί, ωστόσο, ότι ο στοχαστής τη συνέγραψε πολλά χρόνια πριν και υποστηρίζει ότι κυκλοφόρησε (προφανώς αμέσως μετά την ολοκλήρωσή της) δίχως την έγκριση του Ζήνωνα (128
d)· οι παραπάνω ισχυρισμοί, αν και δεν είναι στην ουσία αντιφατικοί, δεν συμφωνούν απόλυτα μεταξύ τους.
Ο Πλάτωνας μας πληροφορεί ότι ο Ζήνωνας με το βιβλίο του αποσκοπούσε στην υπεράσπιση του Παρμενίδη έναντι εκείνων οι οποίοι επιχειρούσαν να καταδείξουν τις παράλογες συνέπειες της παρμενίδειας αντίληψης περί μονισμού. Το βιβλίο περιείχε επιχειρήματα που έδειχναν ότι ακόμη και οι πιο ακραίοι παραλογισμοί προκύπτουν από την αντίπαλη ακριβώς υπόθεση περί πολλαπλότητας παρά από την άποψη των οπαδών του μονισμού (128c-d). Επιβάλλεται, ωστόσο, να διατηρούμε τις επιφυλάξεις μας απέναντι στο ζήτημα. Πράγματι, όλες μας οι πληροφορίες για τον Ζήνωνα επιβεβαιώνουν ότι στην πραγματεία του ανέπτυσσε μια σειρά αποδεικτικούς συλλογισμούς. Ίσως το βιβλίο άφησε αδιευκρίνιστο τον στόχο των επιχειρημάτων του· ο Σωκράτης τον συμπεραίνει αφού έχει ακούσει την ανάπτυξη του συνόλου των επιχειρημάτων (128a-b). Αν ισχύει αυτό, τότε οι ισχυρισμοί του Πλάτωνα συνιστούν ερμηνεία που απαιτεί εξονυχιστική εξέταση.
Στην πραγματικότητα, η πλατωνική ερμηνεία αμφισβητείται από πολλές απόψεις. Η πρώτη και πιο καταφανής απόδειξη είναι η εξής: παρόλο που κατά τον Πλάτωνα ο σκοπός του Ζήνωνα είναι να αποδείξει με το βιβλίο του «αντίθετα προς κάθε παραδοχή ότι τα πράγματα δεν είναι πολλά... και ότι αυτό απο- δεικνύεται από κάθε επιχείρημά του» (127e), πολλά από τα επιχειρήματα στρέφονται όχι κατά της πολλαπλότητας αλλά κατά της κίνησης, ενώ άλλα τείνουν προς άλλους στόχους.
Επιπλέον, ακυρώνεται ο φιλοσοφικός δεσμός που υποτίθεται ότι συνδέει τον Παρμενίδη και τον Ζήνωνα, το γεγονός δηλαδή ότι ενώ ο Παρμενίδης επιχειρηματολόγησε θετικά υπέρ ενός ριζοσπαστικού μονισμού, ο Ζήνωνας υπερασπίστηκε την ίδια θέση βάλλοντας κατά της πολλαπλότητας. Ορισμένοι, μάλιστα, διατύπωσαν μια ακόμη πιο ακραία άποψη, ότι ορισμένα από τα επιχειρήματα του Ζήνωνα στην ουσία στρέφονται όχι μόνο εναντίον των αντιπάλων του αλλά και εναντίον του Παρμενίδη. Η ερμηνεία που επιχειρεί ο Πλάτωνας, αν ισχύουν όλες αυτές οι κατηγορίες, αποδεικνύεται μοιραία ανεπαρκής, και ό,τι απομένει από τον Ζήνωνα είναι μια σειρά επιχειρήματα άνισης αξίας καθένα από τα οποία αξίζει να υποβληθεί σε αυτόνομη διερεύνηση, καθώς η συνεξέτασή τους συνολικά δεν προσθέτει τίποτε.
Στη συνέχεια, θα επιχειρήσω να αντιπαρατεθώ με την τρέχουσα αυτή ερμηνεία. Αν λάβουμε ως δεδομένο πως ό,τι έχει σημασία από τον Ζήνωνα έγκειται κυρίως στα μεμονωμένα επιχειρήματά του, και αν επίσης λάβουμε υπόψη μας ότι το σημείο επαφής Ζήνωνα και Παρμενίδη απαιτεί διερεύνηση, είναι πολλά αυτά που απομένουν να ειπωθούν αναφορικά με τον ισχυρισμό του Πλάτωνα ότι ο σκοπός του Ζήνωνα ήταν να πληρώσει με το ίδιο νόμισμα εκείνους που αποτόλμησαν να γελοιοποιήσουν την ελεατική φιλοσοφία.
ΤΟ ΠΡΩΤΟ ΠΑΡΑΔΟΞΟ ΤΟΥ ΖΗΝΩΝΑ
Το βιβλίο του Ζήνωνα που μνημονεύει ο Πλάτωνας περιείχε σαράντα επιχειρήματα κατά της πολλαπλότητας. Δεν είναι πάντοτε σαφές τι θεωρείται Ζηνώνειο επιχείρημα· από μια εύλογη, ωστόσο, μέτρηση προκύπτει ότι σώζονται δώδεκα περίπου επιχειρήματα εκ των οποίων μόνο τα μισά στρέφονται άμεσα κατά της πολλαπλότητας.
Κατά τον Πλάτωνα, το πρώτο επιχείρημα περιγράφεται ως εξής: «Αν τα όντα είναι πολλά, πρέπει τότε να είναι όμοια και συνάμα ανόμοια· αυτό, όμως, είναι αδύνατο, καθώς ούτε τα ανόμοια μπορούν να είναι όμοια ούτε τα όμοια ανόμοια» (Παρμενίδης 127e) [Εί πολλά έστι τά όντα, ώς άρα δει αυτά δμοιά τε είναι καί άνόμοια, τοϋτο δέ δή άδύνατον · οϋτε γάρ τά ανόμοια δμοια οϋτε τά δμοια άνόμοια οιόν τε είναι]. Σύμφωνα με την πλατωνική ερμηνεία, το επιχείρημα του Ζήνωνα συνίσταται στην εξής υπόθεση: αν τα όντα ήσαν πολλά, θα είχαν άτοπα γνωρίσματα· συνεπώς τα όντα δεν είναι πολλά. Διευρύνει, μάλιστα, το επιχείρημα καθώς θεωρεί ότι ο Ζήνωνας προασπίζεται τον παρμενίδειο μονισμό.
Θα επιχειρήσω να προσεγγίσω τα παραπάνω σημεία ακολουθώντας αντίστροφη σειρά. Καταρχήν, όσον αφορά τον μονισμό, ορισμένοι θεωρούν ότι ο Παρμενίδης δεν ήταν καν μονιστής και συνεπώς η πλατωνική ερμηνεία του Ζήνωνα αποδεικνύεται απολύτως εσφαλμένη. Δεν αποδέχομαι την εν λόγω αντιμετώπιση του Παρμενίδη αλλά ο διαθέσιμος χώρος δεν μου επιτρέπει να εκφράσω την αντίθεσή μου αναλυτικά. Έχει, επίσης, διατυπωθεί η άποψη ότι ο μονισμός και η πολλαπλότητα δεν εκπροσωπούν τις μόνες πιθανές θεωρίες· η απόρριψη της μιας δεν συνεπάγεται την αποδοχή της άλλης. Τον 5ο αι. π.Χ. ο Γοργίας προτείνει μια τρίτη πιθανή εκδοχή, ότι δεν υπάρχει τίποτε. Θεωρώ ότι πρόκειται για άποψη λογικά ορθή αλλά όχι πειστική. Σημασία δεν έχει αν με τυπικά κριτήρια ισχύουν και άλλες πιθανές απόψεις, αλλά ποιες ιδέες κυκλοφορούσαν την εποχή αυτή και ποιες αποτελούσαν στόχο του Ζήνωνα. Όσον αφορά τη χρονολόγηση είναι δύσκολο να πιστέψουμε ότι ο Γοργίας πρότεινε τη θεωρία του πριν ο Ζήνωνας συγγράψει το βιβλίο του και δεν συντρέχει κανένας λόγος για να υποθέσουμε ότι όταν ο στοχαστής ξεκίνησε τη συγγραφή του βιβλίου του, η θεωρία του μηδενισμού ήταν ήδη διαδεδομένη. Επιπλέον, αν οι αντίπαλοι του Ζήνωνα ήσαν «υποστηρικτές της πολλαπλότητας» (128d) [οί πολλά λέγοντες] δεν αποτελεί αθέμιτη στρατηγική το εγχείρημα του στοχαστή να αποδείξει ανυπόστατη την άποψή τους. Από τη στιγμή που θα τους αποκόψει από τη θεωρία περί πολλαπλότητας θα φανούν πιο πρόθυμοι να υιοθετήσουν τα επιχειρήματα του Παρμενίδη υπέρ του μονισμού. Πράγματι, ο Πλάτωνας καθιστά σαφές ότι τα επιχειρήματα του Ζήνωνα δεν ισοδυναμούν με απόπειρα να αποδειχθεί ότι ισχύει ο μονισμός- όταν ο Σωκράτης υποθέτει ότι ισο- δυναμούν με υπεράσπιση του μονισμού, ο Ζήνωνας απαντά ότι δεν συμβαίνει αυτό, αλλά ότι απλώς και μόνο στρέφονται κατά της πολλαπλότητας (128b-d).
Έπειτα, ο Πλάτωνας αποκαλύπτει ότι το επιχείρημα του Ζήνωνα αποδει- κνύεται από τυπική άποψη ατελές. Ο Ζήνωνας πρεσβεύει ότι αν (α) τα όντα είναι πολλά, τότε (β) είναι συνάμα όμοια και ανόμοια· η δεύτερη, ωστόσο, προκεί- μενη δεν ισχύει. Στη συνέχεια, όχι ο Ζήνωνας αλλά ο Σωκράτης συνάγει το συμπέρασμα ότι εφόσον αποκλείεται να ισχύει η δεύτερη προκείμενη αυτό συνεπάγεται ότι δεν ισχύει ούτε η πρώτη προκείμενη. Ο τελικός αυτός συλλογισμός συνιστά αντιπροσωπευτικό γνώρισμα των επιχειρημάτων εκείνων που είναι γνωστά ως επιχειρήματα της εις άτοπον απαγωγής. Για να αποδείξουμε ότι το x δεν ισχύει, αρκεί να δείξουμε ότι το x συνεπάγεται το ψ, το οποίο δεν ισχύει ή είναι αδύνατο· και καθώς το ψ δεν ισχύει ή είναι αδύνατο, συνάγεται το συμπέρασμα ότι και το x δεν ισχύει. Καθώς όλα τα σωζόμενα επιχειρήματα με τον τρόπο που αναπτύσσονται δείχνουν ότι μια υπόθεση καταλήγει σε ένα συμπέρασμα παράλογο ή άτοπο αλλά ούτε ένα δεν περιέχει την παραπάνω χαρακτηριστική κίνηση, υποστηρίχθηκε ότι ο Ζήνωνας «δεν χρησιμοποιεί την τεχνική της εις άτοπον άπαγωγής ως μέθοδο για την ανασκευή που επιχειρεί». Και αυτός, επίσης, ο ισχυρισμός, μολονότι από λογική άποψη ορθός, δεν είναι ωστόσο πειστικός. Ο Πλάτωνας επισημαίνει με κάθε επιθυμητή σαφήνεια ότι το επιχείρημα αποσκοπεί στην ανασκευή της πρώτης προκείμενης. Αν πράγματι ο Ζήνωνας δεν επιδιώκει να συναγάγει το συμπέρασμα ότι η πρώτη προκείμενη δεν ισχύει, τα συμφραζόμενα του συλλογισμού του φανερώνουν με σαφήνεια ότι αυτό είναι το συμπέρασμα που συνάγεται (ποια άλλη σημασία θα μπορούσε να έχει το επιχείρημα;)· και από τη στιγμή που διαπιστώνουμε ότι η δεύτερη προκείμενη δεν ισχύει, ο Ζήνωνας προσδοκά ότι μόνοι μας εμείς θα φτάσουμε στο συμπέρασμα πως δεν ισχύει η πολλαπλότητα. Το επιχείρημα, αν όχι με τυπικά κριτήρια, υπό ρητορική τουλάχιστον έννοια συνιστά απαγωγή.
Ας έρθουμε στο τρίτο ζητούμενο· ο Πλάτωνας δεν περιγράφει με ποιόν τρόπο ο Ζήνωνας μεταβαίνει από την πρώτη προκείμενη («αν τα όντα είναι πολλά») στη δεύτερη προκείμενη («πρέπει τότε να είναι όμοια και συνάμα ανόμοια»). Επιπλέον, δεν μπορούμε να γνωρίζουμε τι ακριβώς εννοούσε ο στοχαστής με τους όρους «όμοια» και «ανόμοια». Ο λόγος, μάλιστα, για τον οποίο η δεύτερη προκείμενη θεωρείται αδύνατη, όπως αυτός διατυπώνεται στο τρίτο σκέλος του συλλογισμού του («ούτε τα ανόμοια μπορούν να είναι όμοια ούτε τα όμοια ανόμοια») επιδέχεται περισσότερες από μια ερμηνείες. Η κατάσταση της σωζόμενης μαρτυρίας δεν επιτρέπει την αξιόπιστη ανασύνθεση του επιχειρήματος. Σύμφωνα με μια εκδοχή ο συλλογισμός διατυπώθηκε ως εξής: Αν υπάρχουν πολλά πράγματα, τότε υπάρχουν τουλάχιστον δύο. Ας επιλέξουμε, λοιπόν, δύο από αυτά, το Α και το Β. Το Α δεν είναι όμοιο με το Β, καθώς το Α διαφέρει από το Β σε ένα τουλάχιστον σημείο. (Το Α διαφέρει από το Β, αλλά το Β δεν διαφέρει από το Β). Παρόμοια, το Β διαφέρει από το A. Το Α, όμως, είναι όμοιο με το Α (καθώς το Α με κανέναν τρόπο δεν μπορεί να είναι διαφορετικό από το Α), και το Β όμοιο με το Β. Κατά συνέπεια, τα Α και Β είναι συνάμα και όμοια και ανόμοια. Αν αυτό είναι το σκεπτικό του Ζήνωνα, το επιχείρημά του δεν ευσταθεί, καθώς τα Α και Β μπορούν να είναι όμοια και ανόμοια με τον τρόπο που υποδείξαμε. Το υποτιθέμενο άτοπο θα προέκυπτε μόνο αν τα ίδια πράγματα ήταν συνάμα όμοια και ανόμοια με τα ίδια πράγματα από την ίδια άποψη, την ίδια χρονική στιγμή κ.ο.κ. Ίσως ο Ζήνωνας κατέληξε βάσιμα στο συμπέρασμά του· αλλά και αν η υπόθεση ευσταθεί, δεν διαθέτουμε καμία ένδειξη για το πώς κατέληξε στο εν λόγω συμπέρασμα.
Η τέταρτη παρατήρησή μας είναι ότι το επιχείρημα του Ζήνωνα αποτελεί μορφή αντινομίας. Σύμφωνα με αυτήν την ιδιαίτερη μορφή της εις άτοπον απαγωγής το άτοπο προκύπτει από την προκείμενη του συλλογισμού, πράγμα που συνιστά αντίφαση της μορφής «χ και όχι χ». Πρόκειται για μια τυπική μορφή Ζηνώνειου επιχειρήματος. Σύμφωνα με άλλα επιχειρήματα, τα ίδια πράγματα είναι ενκαι πολλά, κινούνται και αδρανούν (Πλάτωνα, Φαιδρός261d). Σε ένα σωζόμενο επιχείρημά του, ο Ζήνωνας διατείνεται ότι αν υπάρχουν πολλά όντα, τότε τα ίδια όντα είναι πεπερασμένα και άπειρα (DK29B3). Ένα άλλο επιχείρημά του καταλήγει στο συμπέρασμα ότι καθένα από τα πολλά όντα είναι συνάμα και μικρό και μεγάλο (εν μέρει το επιχείρημα απαντά στα αποσπάσματα DK29B1-2). Ως αντινομίες, επίσης, μπορούν να ερμηνευθούν τα επιχειρήματα του Ζήνωνα για την κίνηση.
ΕΝΑ ΕΠΙΠΛΕΟΝ ΠΑΡΑΔΟΞΟ ΤΗΣ ΠΟΛΛΑΠΛΟΤΗΤΑΣ
Ο Σιμπλίκιος (Εις τό τής Άριστοτέλους Φυσικής Άκροάσεως Υπόμνημα 97.12-13) παραθέτει την ακόλουθη μαρτυρία του Ευδήμου (DK29A16): «ο Ζήνωνας ισχυριζόταν ότι, αν κάποιος του εξηγούσε τι είναι το ένα, τότε θα ήταν σε θέση να κάνει λόγο για αυτά που υπάρχουν» [καί Ζήνωνά φασι λέγειν, εϊ τις αντφ τό εν άποδοίη τί ποτέ έστιν, εξειν τά όντα λέγειν]. Η πρόκληση που έθετε ο Ζήνωνας στους εκπροσώπους της πολλαπλότητας ήταν η εξής: «Δώστε μου μια συνεπή ερμηνεία ενός από τα πολλά όντα που πρεσβεύετε, και εγώ θα αναγνωρίσω τη θεωρία σας περί πολλαπλότητας». Στη συνέχεια παρουσίαζε τα άτοπα που προκύπτουν από τις διάφορες εκδοχές της πολλαπλότητας.
Ένα από τα επιχειρήματα αυτά,'που προφανώς στρεφόταν εναντίον της άποψης ότι υπάρχουν τρισδιάστατα σώματα, καταλήγει στην αντιφατική θέση ότι αν τα όντα είναι πολλά, τότε είναι συνάμα και μικρά και μεγάλα, και συγκεκριμένα (α) τόσο μικρά σε βαθμό που να μην έχουν κανένα μέγεθος (μικρά μέν, ωστε μή εχειν μέγεθος) και (β) τόσο μεγάλα ώστε να είναι άπειρα (μεγάλα δέ ώστε άπειρα είναι). Ο Ζήνωνας θεωρεί όχι μόνο ότι οι δύο προκείμενες (α, β) αλληλοαποκλείονται αλλά ότι η καθεμιά από αυτές παρουσιάζει τις δικές της σοβαρές δυσκολίες.
Η αιτιολόγηση της πρώτης προκείμενης μας παραδίδεται ατελώς. Πληροφορούμαστε μόνο πως ο Ζήνωνας υποστήριζε ότι καθένα από τα πολλά όντα «ταυτίζεται με τον εαυτό του και με το εν» και με βάση τη θέση αυτή συμπεραίνει ότι κανένα ον δεν έχει μέγεθος. Ισχυρίζεται ότι «κάτι που δεν έχει ούτε μέγεθος ούτε πυκνότητα ούτε όγκο δεν θα μπορούσε να υπάρξει» [οὗ μήτε μέγεθος μήτε πάχος μήτε ὄγκος μηθείς ἔστιν, οὐδ’ ἄν εἴη τοῦτο], Το επιχείρημά του αναπτύσσεται ως εξής:
εἰ γάρ ἄλλῳ ὄντι (...) προσγένοιτο, οὐδέν ἄν μεῖζον ποιήσειεν μεγέθους γάρ μηδενός ὄντος, προσγενομένου δέ, οὐδέν οἷόν τέ εἰς μέγεθος ἐπιδοῦναι. Καί οὕτως ἄν ἤδη τό προσγινόμενον οὐδέν εἴη. εἰ δέ ἀπογινόμενου τό ἕτερον μηδέν ἔλαττον ἔσται μηδέ αὗ προσγινομένου αὐξήσεται, δῆλον ὅτι τό προσγενόμενον οὐδέν ἦν οὐδέ τό ἀπογενόμενον (DK29B2)
[«Γιατί αν το πρόσθετε κανείς σε κάτι άλλο που υπάρχει, δεν θα έκανε αυτό το άλλο μεγαλύτερο· γιατί αν το πρόσθετε χωρίς να έχει κανένα μέγεθος, το προστιθέμενο δεν θα μεγάλωνε καθόλου σε μέγεθος. Και, επομένως, αυτό που θα προσθέταμε δεν θα ήταν στην πραγματικότητα τίποτε. Αν, όμως, όταν αυτό αφαιρείται, το άλλο σώμα δεν μικραίνει ούτε μεγαλώνει από την πρόσθεση, είναι φανερό ότι αυτό που προστέθηκε δεν ήταν τίποτε, όπως τίποτε δεν ήταν και αυτό που αφαιρέθηκε»]
Στη συνέχεια ο Ζήνωνας υπερασπίζεται τη δεύτερη προκείμενη:
εἰ δέ ἔστιν, ἀνάγκη ἕκαστον μέγεθος τί ἔχειν καί πάχος καί ἀπέχειν αὐτοῦ τό ἕτερον ἀπό τοῦ ἑτέρου. Καί περί τοῦ προὔχοντος ὁ αὐτός λόγος. Καί γάρ ἐκεῖνο ἕξει μέγεθος καί προέξει αὐτοῦ τί. ὅμοιον δή τοῦτο ἅπαξ τε εἰπεῖν καί ἀεί λέγειν οὐδέν γάρ αὐτοῦ τοιοῦτον ἔσχατον ἔσται οὔτε ἕτερον πρός ἕτερον οὐκ ἔσται. οὕτως εἰ πολλά ἔστιν, ἀνάγκη αὐτά μικρά τέ εἶναι καί μεγάλα μικρά μέν ὥστε μή ἔχειν μέγεθος, μεγάλα δέ ὥστε ἄπειρα εἶναι. (DK29B1)
[«Αν, όμως, υπάρχει (ή: αν αυτά, τα πολλά όντα υπάρχουν), είναι ανάγκη να έχει το καθένα κάποιο μέγεθος και κάποια πυκνότητα και το ένα μέρος του να απέχει από το άλλο. Και το ίδιο σκεπτικό ισχύει για το μέρος του που προεξέχει- γιατί και εκείνο επίσης θα έχει μέγεθος και ένα μέρος του θα προεξέχει επίσης από αυτό. Και μάλιστα είναι το ίδιο πράγμα αν το πούμε αυτό μία φορά και αν το λέμε συνεχώς· γιατί κανένα κομμάτι του αυτής της μορφής δεν θα είναι το τελευταίο ούτε θα υπάρχει κανένα κομμάτι του αυτής της μορφής που να μη συνδέεται με ένα άλλο. Συνεπώς, αν υπάρχουν πολλά όντα, πρέπει αυτά να είναι συνάμα και μικρά και μεγάλα· τόσο μικρά ώστε να μην έχουν μέγεθος και τόσο μεγάλα ώστε να είναι άπειρα»]
Αν υπάρχουν πολλά όντα, τότε σύμφωνα με το απ. Β2 το καθένα από αυτά έχει μέγεθος. Επιλέγοντας οποιοδήποτε από αυτά μπορούμε να διακρίνουμε ένα μέρος του από το υπόλοιπο. Αυτό το μέρος έχει μέγεθος (διαφορετικά, σύμφωνα με το απ. Β2, δεν θα υπήρχε)· άρα μπορούμε να διακρίνουμε ένα μέρος αυτού του μέρους από το υπόλοιπο. Και αυτό το μέρος, επίσης, έχει μέγεθος. Η διαδικασία αποβαίνει αέναη: ποτέ δεν φτάνουμε σε ένα τελικό υποσύνολο.
Ο Ζήνωνας καταλήγει στην εξής διατύπωση: «αν υπάρχουν πολλά όντα, πρέπει αυτά να είναι τόσο μεγάλα, ώστε να είναι άπειρα». Είναι κοινά παραδεκτή η θέση ότι το επιχείρημα έχει την εξής έννοια: καθετί που έχει πεπερασμένο μέγεθος, περιέχει άπειρα μέρη και καθένα από αυτά έχει πεπερασμένο μέγεθος. Ο Ζήνωνας έσφαλλε όταν υπέθετε ότι το σύνολο ενός άπειρου αριθμού πεπερασμένων μεγεθών πρέπει να είναι άπειρο. Το επιχείρημα όμως δεν στρέφεται προς αυτήν την κατεύθυνση και το συμπέρασμα μπορεί να είναι διαφορετικό. Το πρόβλημα δεν έγκειται στο πώς θα ανασυνθέσουμε το αρχικό ον από τη στιγμή που αυτό κατατμήθηκε σε άπειρα μέρη, αλλά στο πώς θα ολοκληρωθεί η κατάτμηση. Αν η κατάτμηση παύει σε κάποιο σημείο, έτσι ώστε έως έναν βαθμό να εγγίζουμε τα ελάχιστα δομικά μέρη από τα οποία συναπαρτίζεται το αρχικό ον, τότε η επάνοδος στην αρχική του μορφή γίνεται ανέφικτη· αυτά τα δομικά μέρη είναι εκείνα από τα οποία συντίθενται όσα εμείς αποκαλούμε «πολλά». Ο Ζήνωνας, όμως, αποδεικνύει ότι δεν υφίσταται κανένας επαρκής λόγος, ώστε να σταματήσει η κατάτμηση. Οτιδήποτε εκτείνεται στον χώρο μπορεί να κατατμηθεί σε μέρη που και αυτά εκτείνονται στον χώρο· κατά συνέπεια, ποτέ δεν θα είμαστε σε θέση να σταματήσουμε την κατάτμηση. Το συμπέρασμα του Ζήνωνα είναι ότι καθένα από τα πολλά όντα είναι τόσο μεγάλο, ώστε να περιέχει άπειρα μέρη· δεν αναλαμβάνει, ωστόσο, να τοποθετηθεί πάνω στο ζήτημα αν το καθετί που έχει άπειρα μέρη μπορεί να έχει πεπερασμένο μέγεθος.
Αξίζει να σημειώσουμε ότι το επιχείρημα του Ζήνωνα δεν προϋποθέτει την άπειρη διαιρετότητα της ύλης. Είναι σαφές ότι, αν υφίστανται ελάχιστες ενότητες ύλης (όπως για παράδειγμα πρέσβευε η αρχαία Ατομική θεωρία), η διαίρεση των σωμάτων του φυσικού κόσμου λήγει σε ένα συγκεκριμένο σημείο. Το επιχείρημα, όμως, έχει την εφαρμογή του ακόμη και στα μεμονωμένα άτομα. Μπορούμε νοερά να διακρίνουμε το δεξιό από το αριστερό ήμισυ ενός ατόμου και παρόμοια να διακρίνουμε το δεξιό ήμισυ του δεξιού ημίσεως από το αριστερό ήμισυ του δεξιού ημίσεως· έτσι, αυτή η διαδικασία της νοερής ή «θεωρητικής» κατάτμησης αποδεικνύεται ατελεύτητη. Η μόνη προϋπόθεση που προβάλλει το επιχείρημα είναι η υπόθεση ότι η επέκταση στον χώρο είναι συνεχής.
ΤΟ ΑΠΕΙΡΟΝ
Ο τρόπος που αναπτύσσει ο Ζήνωνας την έννοια του απείρου και κάθε σχετικού όρου στο επιχείρημα που μόλις αναλύσαμε και σε ορισμένα προπαντός από τα περίφημα παράδοξό του για την κίνηση στάθηκε η κύρια αιτία του ενθουσιασμού που προκάλεσαν τα παράδοξά του ιδιαίτερα κατά τον εικοστό αιώνα. Σε συγκεκριμένα συμφραζόμενα το άπειρον έχει τη συνήθη για μας σημασία και πολλά από τα επιχειρήματα του Ζήνωνα συνεπάγονται άπειρες αναγωγές στο άπειρο. Επιπλέον, κάποια συγκεκριμένα επιχειρήματα του στοχαστή, όπως η «Διχοτομία», «ο Αχιλλέας», και το «Βέλος», εγείρουν ερωτήματα τα οποία δεν θα μπορούσαν να απαντηθούν πριν από την ανάπτυξη της θεωρίας του μαθηματικού απείρου κατά τον 19ο αι. Το πιο μεγάλο μέρος της έρευνας που συντελέσθηκε κατά τον 20ο αιώνα πάνω στα Ζηνώνεια παράδοξα έχει επικεντρωθεί στην ερμηνεία τους η οποία βασίζεται στην αξιοποίηση της εν λόγω μαθηματικής θεωρίας και των πιθανών φυσικών της εφαρμογών. Θα επιστρέψω σε αυτά τα ζητήματα· στο σημείο αυτό, ωστόσο, πρόθεσή μου είναι να αποδείξω ότι η έρευνα που συντελέσθηκε υπήρξε από μια άποψη αναχρονιστική και στράφηκε προς λάθος κατεύθυνση.
Υπάρχει διαφορά ανάμεσα σε αυτό που εννοούσε ο ίδιος ο Ζήνωνας ή κάθε άλλος φιλόσοφος με τις διατυπώσεις του και σε αυτό που εμείς αντιλαμβανόμαστε με βάση τις διατυπώσεις του. Παρόμοια, ίσως αυτό που εμείς θεωρούμε πρόβλημα ή λύση του προβλήματος δεν ταυτίζεται με ό,τι ο Ζήνωνας θεωρούσε πρόβλημα ή λύση του προβλήματος. Το έργο του φιλοσόφου που αντιμετωπίζει με σοβαρότητα τα Ζηνώνεια παράδοξα και καταδεικνύει τα προβλήματα που ανακύπτουν είναι διαφορετικό από το έργο του ιστορικού της φιλοσοφίας ο οποίος προσπαθεί να κατανοήσει τι εννοούσε ο Ζήνωνας με τα παράδοξα του και ποιες λύσεις θα ήταν ικανοποιητικές για τον ίδιο. Από την εποχή τουλάχιστον του Αριστοτέλη, οι φιλόσοφοι αντιμετώπιζαν τα παράδοξα ως γρίφους που επιζητούσαν λύση και οι λύσεις που πρότειναν κατά κανόνα συνεπάγονταν άγνωστες στον Ζήνωνα θεωρίες, εννοιολογικές συλλήψεις και διακρίσεις. Αξίζει να σημειώσουμε ότι ο Ζήνωνας ήταν σε θέση να διατυπώνει γρίφους που αφορούν τον πυρήνα των εννοιολογικών συλλήψεων του χώρου, του χρόνου και της κίνησης, πράγμα που συνιστά επαρκή λόγο για να εξετάσουμε τις Ζηνώ- νειες διατυπώσεις υπό το φως των δικών μας θεωριών. Επιβάλλεται, επίσης, να λαμβάνουμε υπόψη τις διακρίσεις που θέσαμε παραπάνω· η συχνή παράλειψη των ιστορικών της φιλοσοφίας και των φιλοσόφων να το πράξουν, κατέστησαν τον Ζήνωνα τον πλέον παρερμηνευμένο στοχαστή.
Όσον αφορά τον αξονικής σημασίας όρο άπειρον, είναι βέβαιο ότι στα χρόνια του Ζήνωνα δεν είχε την προφανή σημασία που έχει σήμερα. Πρόκειται για σύνθετη λέξη με α' συνθετικό το στερητικό α- και β' συνθετικό είτε το ουσιαστικό πέρας (=«όριο», «σύνορο»), οπότε στην περίπτωση αυτή σημαίνει «απεριόριστο», «δίχως όρια», «άπειρο», είτε τη ρίζα περ- («διά μέσου», «πέρα από», «προς τα εμπρός»), οπότε σημαίνει «αυτό που δεν διανύεται» ή «αυτό από το ένα άκρο του οποίου είναι αδύνατο να μεταβεί κάποιος στο άλλο». Ο Ζήνωνας αντιπαραθέτει στο άπειρον το πεπερασμένον (Β3)· στον Αριστοτέλη οι όροι έχουν τη σημερινή σημασία. Ο Αριστοτέλης ανέπτυξε μια θεωρία περί απείρου με ορισμένες τεχνικές λεπτομέρειες, και την έστρεψε εναντίον του Ζήνωνα· ο πέμπτος αιώνας, όμως, δεν ήταν εξοικειωμένος με τεχνικές λεπτομέρειες αυτού του τύπου. Στον αιώνα αυτόν, με τον όρο άπειρον, οι άνθρωποι εννοούσαν το «ανεξάντλητο», το «αχανές», το «ατελεύτητο», όπως τον «άπειρο ψηλό αιθέρα» [τόν ύψοϋ τόνδ’ άπειρον αιθέρα] (Ευριπίδη απ. 941) ή «την απέραντη πεδιάδα που απλώνεται μέχρι εκεί που μπορεί να φτάσει το μάτι του ανθρώπου» (Ηροδότου 1.204). Συγκεκριμένα, εξ ορισμού ό,τι είναι άπειρον δεν έχει κανένα όριο· από την άποψη αυτή, ό,τι ο Ζήνωνας θεωρεί άπειρον είναι ριζικά διαφορετικό από αυτό που εμείς αντιλαμβανόμαστε ως άπειρον και ειδικότερα από ορισμένες άπειρες ακολουθίες. Συνηθίζουμε να θεωρούμε ότι η άπειρη ακολουθία 1/2,1/4,1/8 ... δεν έχει κανέναν τελικό όρο· έχει όμως ένα όριο, το μηδέν (0)· από την άλλη, συνήθως θεωρούμε κατά παρόμοιο τρόπο ότι η άπειρη ακολουθία των μερικών αθροισμάτων 1/2, 3/4, 7/8 δεν έχει κανέναν τελικό όρο· έχει όμως ένα πεπερασμένο όριο, τη μονάδα (1). Σύμφωνα με τον Ζήνωνα, οι αντίστοιχες σκέψεις που πλαισιώνονται με όρους του απείρου θα αποδεικνύονταν αντιφατικές. Ο στοχαστής υποστηρίζει ότι είναι αδύνατο να εκτελεσθεί μια άπειρη σειρά πράξεων, μια σειρά που εξ ορισμού δεν έχει κανένα όριο. Στην άποψη ότι οι μαθηματικοί αποδεικνύουν ότι αυτό είναι δυνατό αν ορίσουμε το άθροισμα της αρχικής άπειρης ακολουθίας ως το όριο των μερικών αθροισμάτων, χρειάζεται να δοθεί η εξής απαξιωτική απάντηση: «Η θέσπιση ενός ορισμού δεν καθιστά τίποτε δυνατό, ιδιαίτερα μάλιστα όταν ο ορισμός συνιστά αντίφαση! Ό,τι χαρακτηρίζεται ως άπειρον, δεν έχει κανένα όριο. Η απλή διακήρυξη ότι ορισμένα άπειρα πράγματα έχουν όρια, δεν τα καθιστά πεπερασμένα».
Δεν πρόκειται, ασφαλώς, για οριστική διευθέτηση του ζητήματος· γίνεται, ωστόσο, φανερό ότι από τη στιγμή που η Ζηνώνεια σύλληψη του απείρου δεν συμπίπτει με τη δική μας, η διατύπωση του παραδόξου με όρους του απείρου και η επίλυσή του με βάση τους όρους αυτούς ισοδυναμεί με διατύπωση και επίλυση ενός διαφορετικού παραδόξου. Αυτό δεν σημαίνει ότι είναι τελείως ανέφικτη η προσέγγιση που περιγράφουμε- χρειάζεται μόνο να επιδεικνύουμε προσοχή σε κάθε μας βήμα όταν πραγματευόμαστε αρχαία παράδοξα με σύγχρονες μεθόδους. Πράγματι, η σύλληψη του απείρου από τους ειδικούς της εποχής μας υπερέχει έναντι της Ζηνώνειας σύλληψης. Για παράδειγμα, η σύγχρονη έρευνα, αντίθετα από τον Ζήνωνα, διακρίνει διαφορετικά μεγέθη απείρου, μας επιτρέπει να προχωρούμε σε μαθηματικές πράξεις με άπειρες ποσότητες, αυτές να τις συγκρίνουμε με ακρίβεια και να προσδιορίζουμε διαφορετικές παραμέτρους από τις οποίες κάτι ενδέχεται να θεωρηθεί άπειρο. Ενώ ο Ζήνωνας διακήρυσσε απερίφραστα ότι είναι αδύνατο να εκτελεσθεί μια άπειρη σειρά πράξεων, σήμερα εμείς γνωρίζουμε ότι ορισμένες άπειρες σειρές πράξεων εκτελούνται ενώ άλλες όχι και είμαστε και σε θέση να εξηγήσουμε το φαινόμενο. Στην ενότητα που ακολουθεί επιχειρούμε να δείξουμε πώς οι παραπάνω παρατηρήσεις εφαρμόζονται στα παράδοξα της κίνησης.
ΤΑ ΕΠΙΧΕΙΡΗΜΑΤΑ ΚΑΤΑ ΤΗΣ ΚΙΝΗΣΗΣ
Σύμφωνα με τον Αριστοτέλη (Φυσικά 6 9. 239b9, DK29A25) «τέσσερα είναι τα επιχειρήματα του Ζήνωνα για την κίνηση που προκαλούν δυσκολίες σε όσους προσπαθούν να τα ερμηνεύσουν» [τέτταρες δ' είσίν οί λόγοι περί κινή- σεως Ζήνωνος οί παρέχοντες τάς δυσκολίας τοΐς λύουσιν]. Ο συγγραφέας των Φυσικών παραθέτει την τετράδα των πλέον δυσερμήνευτων έως τις μέρες μας παραδόξων, τα οποία, όπως όλα δείχνουν, θα παραμείνουν δυσερμήνευτα. Δεν είναι βέβαιο αν τα επιχειρήματα αυτά συγκαταλέγονταν στα σαράντα επιχειρήματα κατά της πολλαπλότητας. Αν δεν συγκαταλέγονταν, τότε το βιβλίο του Ζήνωνα που μνημονεύει ο Πλάτωνας δεν περιείχε το σύνολο των Ζηνώνει- ων παραδόξων· αν συγκαταλέγονταν, τότε κρίνεται αμφίβολη η αναφορά του Πλάτωνα ότι όλα τα παράδοξα του βιβλίου στρέφονταν κατά της πολλαπλότητας, αν και όχι τόσο αμφίβολη όσο θεωρούν ορισμένοι, καθώς η έννοια της κίνησης συνεπάγεται μια πολλαπλότητα χωρικών και χρονικών σημείων. Όπως είδαμε, μάλιστα, δεν υπάρχει αμφιβολία ότι ένα από τα παράδοξα βάλλει κατά της πολλαπλότητας και βασίζεται σε υποθέσεις που αφορούν τον χώρο.
Από τυπική άποψη ο Αριστοτέλης αντιμετωπίζει τα παράδοξα ως αινίγματα που επιζητούν λύση· δεν σκοπεύει να τα κατανοήσει με κριτήριο τους όρους που θέτει ο Ζήνωνας. Τα συνοψίζει επιγραμματικά και προτείνει τις δικές του λύσεις, οι περισσότερες από τις οποίες βασίζονται σε έννοιες που ανέπτυξε ο ίδιος και τις οποίες δεν γνώριζε ο Ζήνωνας. Θα πραγματευθώ τρία από τα τέσσερα παράδοξα, αρχίζοντας με τη «Διχοτομία» και τον «Αχιλλέα», με τους συλλογισμούς που ο Αριστοτέλης θεωρεί ταυτόσημους (DK29A26) [δεύτερος δ’ ὁ καλούμενος Ἀχιλλεύς…ἔστι δέ καί οὗτος ὁ αὐτός λόγος τῷ διχοτομεῖν].
«Η Διχοτομία»
«Ο πρώτος συλλογισμός απορρίπτει την ύπαρξη κίνησης, γιατί το κινούμενο πρέπει πρώτα να φτάσει στο μέσο της διαδρομής, πριν φτάσει στο τέρμα (Φυσικά 6. 9 239b 11, DK29A25) [πρῶτος μέν ὁ περί τοῦ μή κινεῖσθαι (ενν. λόγος) διά τό πρότερον εἰς τό ἥμισυ δεῖν ἀφικέσθαι τό φερόμενον ἤ πρός τό τέλος]. Είναι κάθε φορά απαραίτητο να διασχίσει κανείς το ήμισυ της διαδρομής, αλλά το ήμισυ αυτό είναι άπειρον και δεν είναι δυνατόν να διέρχεται κανείς από άπειρα πράγματα» (Φυσικά 8. 8 263a5).
«Ο Αχιλλέας»
«Ο πιο γρήγορος δρομέας δεν μπορεί ποτέ να ξεπεράσει τον πιο αργό· γιατί ο διώκτης πρέπει πρώτα να φτάσει στο σημείο από όπου ξεκίνησε ο διωκόμενος, και επομένως ο βραδύτερος δρομέας έχει κάθε στιγμή κάποιο προβάδισμα» (Φυσικά 6. 9 239b 14). [τό βραδύτατον ουδέποτε καταληφθήσεται θέον υπό τοϋ ταχίστου· έμπροσθεν γάρ όναγκαϊον έλθεΐν τό διωκον, δθεν ωρμησε τό φεΰγον, ωστ’ άεί τι προέχειν άναγκαϊον τό βραδύτερον].
Ο Αριστοτέλης θεωρεί ότι ο «Αχιλλέας» συνιστά συλλογισμό ταυτόσημο με τη «Διχοτομία» αλλά διαφέρει από αυτή στο γεγονός ότι το διαιρούμενο μέγεθος δεν διχοτομείται (Φυσικά 6. 239Μ8-20) [έστι δέ καί οϋτος ό αυτός λόγος τφ διχοτομεΐν, διαφέρει δ’ έν τφ διαιρειν μή δίχα τό προσλαμβανόμενον μέγεθος], Ο Αριστοτέλης επιλύει και τα δύο παράδοξα με βάση τη διάκριση που θέτει μεταξύ του απείρου στην έκταση ή στην ποσότητα και του απείρου που προκύπτει από τη διαίρεση:
«δεν μπορεί ένα πράγμα σε πεπερασμένο χρόνο να έρθει σε επαφή με πράγματα που είναι ποσοτικά άπειρα· μπορεί όμως σε πεπερασμένο χρόνο να έρθει σε επαφή με πράγματα άπειρα από την άποψη της διαιρετότητας· γιατί υπό την έννοια αυτή [υπό την έννοια της διαιρετότητας] και ο χρόνος είναι άπειρος. Προκύπτει, συνεπώς, ότι το άπειρο διανύεται σε άπειρο και όχι σε πεπερασμένο χρόνο και η επαφή με τα άπειρα συντελείται σε άπειρους και όχι πεπερασμένους χρόνους» (Φυσικά 6. 2 233a26-31) [των μέν ούν κατά ποσόν άπειρων ούκ ένδέχεται άψασθαι έν πεπερασμένα) χρόνω, των δέ κατά διαίρεσιν ενδέχεται· καί γάρ αυτός ό χρόνος οϋτως άπειρος, ώστε έν τφ άπείρω καί ούκ έν τφ πεπερασμένα) συμβαίνει διιέναι τό άπειρον, καί απτεσθαι των άπειρων τοϊς άπείροις, ου τοϊς πεπερασμένοις].
Και τα δύο παράδοξα, παρόλο που μπορούμε να τα πραγματευθούμε κατ’ αυτόν τον τρόπο, εμφανίζουν σημαντικές διαφορές ακόμα και στο πλαίσιο της συνοπτικής αριστοτελικής έκθεσής τους. Η «Διχοτομία» βασίζεται ρητά σε μια υποτιθέμενη ιδιότητα του απείρου, ενώ ο «Αχιλλέας» δεν περιέχει αναφορά στο άπειρο αλλά βασίζεται στους προσδιορισμούς άεί και ουδέποτε- με τη μορφή που παραδίδονται τα παράδοξα, επιδέχονται και διαφορετικές αναλύσεις· θα επιχειρήσω να τα πραγματευθώ ξεχωριστά.
Η ΔΙΧΟΤΟΜΙΑ
Ό,τι ακολουθεί είναι μια ανεπτυγμένη εκδοχή της «Διχοτομίας»:
«Δεν υφίσταται κίνηση υπό καμία έννοια. Η κίνηση προϋποθέτει τη μετάβαση από έναν τόπο σε έναν άλλον. Ας εξετάσουμε, για παράδειγμα, την κίνηση κατά μήκος ενός σταδίου. Για να διατρέξουμε την απόσταση από το σημείο εκκίνησης (A) έως το σημείο τερματισμού (Β), πρέπει, πρώτα να φτάσουμε στο σημείο Α,, στο μέσο του διαστήματος ΑΒ. Για να μεταβούμε, όμως, από το Α, στο Β πρέπει πρώτα να φτάσουμε στο σημείο Α2, στο μέσο του διαστήματος Α,Β κ.ο.κ. Κάθε φορά που φτάνουμε στο μέσο ενός διαστήματος απομένει να διανύσουμε ακόμη ένα διάστημα που και αυτό με τη σειρά του έχει μέσο. Συνεπώς, προκύπτει άπειρος αριθμός διαστημάτων που πρέπει να διανύσουμε. Δεν είναι, όμως, εφικτό να διανύσουμε άπειρο αριθμό διαστημάτων. Αρα, δεν μπορούμε ποτέ να καταλήξουμε στο σημείο τερματισμού».
Σύμφωνα με μια εναλλακτική ερμηνεία, ο Ζήνωνας υποστηρίζει ότι για να φτάσουμε στο σημείο Α,, πρέπει πρώτα να φτάσουμε στο μέσο του διαστήματος ΑΑ, κ.ο.κ. Η διαφορά μεταξύ των δύο προτεινόμενων ερμηνειών μπορεί να διατυπωθεί με ρητορικό τρόπο ως εξής: βάσει της πρώτης εκδοχής η κίνηση είναι αδύνατο να ολοκληρωθεί, ενώ βάσει της δεύτερης είναι αδύνατο να ξεκινήσει. Σε κάθε περίπτωση, το συμπέρασμα παραμένει το ίδιο: η κίνηση αποδει- κνύεται αδύνατη, καθώς κάθε κίνηση συνεπάγεται την εκτέλεση μιας άπειρης ακολουθίας πράξεων.
Ο Ζήνωνας απορρίπτει την ιδέα ότι υπάρχει κίνηση. Ίσως δεν είναι άτοπο να εικάσουμε ότι η «Διχοτομία» συνιστούσε μέρος μιας αντινομίας: α) Αν υπάρχει κίνηση, τότε η κίνηση από το σημείο Α στο σημείο Β υποδιαιρείται σε έναν πεπερασμένο αριθμό βαθμιδών (Αυτή είναι η άποψη που προκύπτει από την καθημερινή μας εμπειρία. Για παράδειγμα η απόσταση των 100 μέτρων καλύπτεται αφού γίνουν 100 βήματα του ενός μέτρου), β) Αν υπάρχει κίνηση, τότε η κίνηση από το σημείο Α στο σημείο Β περιέχει άπειρο αριθμό βαθμιδών (Η άποψη αυτή προκύπτει από την περιγραφή της κίνησης στον συλλογισμό της «Διχοτομίας»).
Είτε συσταθεί είτε όχι η παραπάνω υποθετική ανασύνθεση, ο Ζήνωνας, με το επιχείρημα της «Διχοτομίας», πρεσβεύει ότι μια πεποίθηση αντίθετη προς την παρμενίδεια άποψη για την ακινησία του όντος, συνεπάγεται από λογική άποψη κάτι το άτοπο. Όποιος πιστεύει ότι υπάρχει κίνηση, πιστεύει υποχρεωτικά ότι είναι δυνατό να φτάσει στο τέρμα μιας ατελεύτητης ακολουθίας επι μέρους κινήσεων· με άλλα λόγια, ότι είναι σε θέση να ολοκληρώσει μια μη ολοκληρώσιμη ακολουθία, να φτάσει στο έσχατο όριο μιας άπειρης ακολουθίας. Αυτό όμως κρίνεται απολύτως ανέφικτο. Αν η ακολουθία είναι ατελεύτητη ή μη ολοκληρώσιμη ή άπειρη, τότε δεν έχει κανένα τέλος, κανένα όριο κ.ο.κ.· επομένως, σε καμία περίπτωση δεν μπορούμε να φτάσουμε στο τέρμα της.
Για να αντικρούσουμε το συμπέρασμα του Ζήνωνα, πρέπει να δείξουμε ότι δεν ισχύει το αδύνατο της κίνησης. Μια απάντηση είναι αυτή του Αντισθένη του κυνικού, ο οποίος σύμφωνα με μαρτυρία του Ηλία (Έξήγησις των δέκα κατηγοριών τής φιλοσοφίας τον θεοφιλεστάτου Φιλοσόφου 109. 20-22) «επειδή αδυνατούσε να ανασκευάσει τα επιχειρήματα του Ζήνωνα κατά της κίνησης, σηκώθηκε όρθιος και έκανε ένα βήμα με το σκεπτικό ότι η παρουσίαση του προφανούς ήταν πιο ισχυρή από κάθε αντιπαράθεση επιχειρημάτων»· πρόκειται για κωμικό και ανεπαρκές εγχείρημα ανασκευής του παραδόξου, αφού ο Ζήνωνας δεν αρνιόταν ότι οι αισθήσεις παρέχουν την πληροφορία πως υπάρχει κίνηση. (Συνεπώς, οι Ελεάτες απέρριπταν τη μαρτυρία των αισθήσεων ως αναξιόπιστη.) Η απλή προσαγωγή ενός ακόμη προφανούς παραδείγματος για την ύπαρξη της κίνησης, παραδείγματος που ο Ζήνωνας θα αποδείκνυε ότι στην πραγματικότητα δεν ισχύει, σημαίνει ότι ο Αντισθένης είτε παρερμήνευσε παντελώς τη θέση του Ζήνωνα είτε ένιωσε την ανάγκη να αποδείξει (στον εαυτό του τουλάχιστον αν όχι στον Ζήνωνα) ότι ακόμη μπορούσε να κινείται.
Το συμπέρασμα του Ζήνωνα για το αδύνατο της κίνησης αντικρούεται, επίσης, αν αποδείξουμε ότι η περιγραφή του στοχαστή είναι παραπλανητική. Το παράδοξο ισχύει μόνο αν αληθεύει το γεγονός ότι πρέπει να φτάσουμε στο μέσο του διαστήματος προτού φτάσουμε στο τέλος του ή ότι κάθε φορά που φτάνουμε στο μέσο, αυτό που απομένει είναι ένα διάστημα στο μέσο, επίσης, του οποίου πρέπει να φτάσουμε προτού διανύσουμε πάλι το διάστημα που απομένει. Η περιγραφή, ωστόσο, του Ζήνωνα δεν επιδέχεται καμία ένσταση: για να διανύσουμε τη συνολική απόσταση, πρέπει να διανύσουμε το ήμισύ της, τα 3/4 κ.ο.κ. Όσο ο χώρος παραμένει συνεχής, όσο εμείς (ενδεχομένως μαζί με τους αντιπάλους του Ζήνωνα) γνωρίζουμε από διαίσθηση, και όσο η σύγχρονη φυσική επιστήμη δεν προβάλλει καμία αντίρρηση, η ακολουθία αυτή θα παραμένει ατελεύτητη.
Το συμπέρασμα του Ζήνωνα αντικρούεται, επίσης, αν δείξουμε ότι, μολονότι η περιγραφή του στοχαστή δεν είναι στην ουσία παραπλανητική, δεν είναι ωστόσο διαφωτιστική· θα ήταν περισσότερο διαφωτιστική αν όριζε ότι για να φτάσουμε στο τέρμα του διαστήματος πρέπει να διανύσουμε έναν συγκεκριμένο αριθμό βημάτων - έργο που περατώνεται χωρίς δυσκολία. Στην ένσταση αυτή υπόκειται η ιδέα ότι η κίνηση είναι δυνατή αν ισχύει κάποια περιγραφή που να μην συνεπάγεται το αδύνατο της κίνησης. Η προσέγγιση, όμως, αυτή χρεώνει άδικα στον Ζήνωνα σκέψεις που ο ίδιος δεν έκανε. Ο στοχαστής δεν ισχυρίζεται ότι κάθε ορθή περιγραφή της κίνησης οδηγεί σε αντίφαση, αλλά μόνο ότι μία τουλάχιστον ορθή περιγραφή καταλήγει πράγματι σε αντίφαση.
Επιπλέον, όταν επισημαίνουμε ότι μπορεί η περιγραφή της κίνησης να είναι ορθή χωρίς να καταλήγει σε αντίφαση, στην πραγματικότητα συνυπογράφουμε την εκδοχή του Ζήνωνα. Τώρα πλέον ο στοχαστής είναι σε θέση να υποστηρίξει ότι η ύπαρξη της κίνησης περιέχει την αντινομία που περιγράψαμε παραπάνω: είναι εξίσου δυνατό (σύμφωνα με την επισήμανσή μας) όσο και αδύνατο (σύμφωνα με το επιχείρημα της «Διχοτομίας») να διανυθεί κάθε δεδομένη απόσταση. Πρόκειται για αντίφαση η οποία ανασκευάζει την προκείμενη που πρεσβεύει την ύπαρξη της κίνησης.
Σε κάθε περίπτωση, ο Ζήνωνας αποδέχεται την εναλλακτική αυτή περιγραφή. Αν απαιτούνται 100 βήματα για να φτάσουμε στο σημείο τερματισμού, πρέπει πρώτα να καλύψουμε μια απόσταση 50 βημάτων, έπειτα 25, στη συνέχεια 12'/2 κ.ο.κ. Ο αντίπαλός του θα αντέτεινε την εξής σκέψη: η περιγραφή του Ζήνωνα δεν προβλέπει κλασματικά βήματα. Ο Ζήνωνας, ωστόσο, μπορεί να συμφωνήσει ότι ένα κλασματικό βήμα δεν συνιστά βήμα (τα 12‘Λ βήματα δεν είναι 12 πλήρη βήματα συν ένα βραχύτερο, 13 δηλαδή στο σύνολό τους βήματα) αλλά μπορεί παράλληλα και να υποστηρίζει ότι ένα βήμα σημαίνει πως μετακινούμε το πόδι μας από το σημείο Α στο σημείο Β, και ότι κατά την μετακίνηση αυτή το πόδι κινείται πρώτα προς το μέσο του διαστήματος ΑΒ κ.ο.κ. με αποτέλεσμα το φάσμα της αναγωγής στο άπειρο να προβάλει ακόμα πιο απειλητικό. Στο σημείο αυτό βρίσκει εφαρμογή η πρόκληση που έθετε ο Ζήνωνας στους εκπροσώπους της πολλαπλότητας να καταθέσουν μια συνεπή ερμηνεία ενός από τα πολλά όντα που πρέσβευαν. Δεν αρκεί να ισχυρίζεται κανείς ότι η κίνηση μπορεί να περιγράφει ως απόσταση 100 βημάτων, όπου ως βήμα νοείται η μονάδα κίνησης. Όταν ο Ζήνωνας επικεντρώνει τη θεώρησή του εναντίον αυτής της μονάδας κίνησης, κάθε αντίθετο επιχείρημα καταρρέει.
Μπορούμε, επίσης, να δεχθούμε ότι πρέπει να διασχίσουμε άπειρα διαστήματα για να μεταβούμε από το σημείο Α στο σημείο Β, αντιτείνοντας, ωστόσο, ότι ο Ζήνωνας σφάλλει όταν υποθέτει πως απαιτείται άπειρος χρόνος για να διανυθούν όλα αυτά τα διαστήματα. Θα μπορούσαμε ίσως, χωρίς να αλλοιώνεται το περιεχόμενο του επιχειρήματος, να αντικαταστήσουμε τον προσδιορισμό «άπειρο» με τον προσδιορισμό «απεριόριστο». Είναι σαφές ότι αν απαιτείται ο ίδιος χρόνος για να διασχίσει κανείς καθένα από τα άπειρα διαστήματα, τότε ο συνολικός χρόνος θα είναι άπειρος. Έτσι ερμήνευσε το παράδοξο ο Αριστοτέλης και το έλυσε με τη διάκριση ανάμεσα στο άπειρο από την άποψη της διαι- ρετότητας και στο άπειρο από την άποψη της έκτασης. Η «Διχοτομία» θεμελιώνεται πάνω στην άπειρη διαιρετότητα της απόστασης και της κίνησης και δεν υποδηλώνει ότι η συνολική απόσταση είναι άπειρη στην έκταση. Ούτε συντρέχει κανένας λόγος να υποθέτουμε ότι ο απαιτούμενος χρόνος είναι άπειρος από την άποψη της διαιρετότητας. Αν απαιτείται μισό λεπτό για να διανυθεί το ήμισυ της απόστασης, τότε ο απαιτούμενος χρόνος για την κάλυψη του 1/4 της απόστασης θα είναι το 1/4 του λεπτού κ.ο.κ. Συνεπώς, όταν η συνολική απόσταση που διανύθηκε είναι πεπερασμένη, τότε και ο συνολικός χρόνος που παρήλθε είναι επίσης πεπερασμένος. Ωστόσο, η «Διχοτομία» δεν προϋποθέτει ότι απαιτείται άπειρος χρόνος για την κάλυψη της απόστασης. Ο συλλογισμός βασίζεται στην υπόθεση ότι είναι αδύνατο να διέλθει κανείς από άπειρα σημεία (DK29A25) [τά άπειρα διελθεϊν], όχι να διέλθει από αυτά σε πεπερασμένο χρόνο. Ως εκ τούτου, η ένσταση που εγείρει ο Αριστοτέλης αλλά και η λύση που προτείνει αποδεικνύονται ανεπιτυχείς καθώς χρεώνουν στον Ζήνωνα ένα σφάλμα στο οποίο δεν συντρέχει κανένας λόγος να υποθέσουμε ότι υπέπεσε ο στοχαστής.
Αφού παραμερίσαμε τις παραπάνω ενστάσεις, ας εξετάσουμε το σκεπτικό του Ζήνωνα. Σύμφωνα με την αριστοτελική μαρτυρία το επιχείρημα περιέχει τρεις προκείμενες:
1. Είναι πάντοτε απαραίτητο να διανύεται το ήμισυ της απόστασης.
2. Τα ημίσεα των αποστάσεων είναι άπειρα.
3. Είναι αδύνατο να διανυθούν άπειρα διαστήματα.
Συνεπώς:
4. Δεν είναι δυνατόν να διανυθεί η συνολική απόσταση.
Η εκτενής ερμηνεία που προτάξαμε στην αρχή της παρούσας ενότητας απο- τελεί επαναδιατύπωση των προκείμενων κατά τρόπο που να συνάγεται εύλογα το παραπάνω συμπέρασμα (4). Θεωρώ ότι οι αντίπαλοι του Ζήνωνα θα συμφωνήσουν με τις προκείμενες (1) και (2). Το ερώτημα όμως είναι αν θα συμφωνήσουν και πάλι με την προκείμενη (3).
Στο σημείο αυτό χρήσιμο είναι να συναγάγουμε στην ανάλυσή μας την έννοια του μαθηματικού απείρου. Ο λόγος είναι ότι η Ζηνώνεια εκδοχή του προβλήματος, που από λογική άποψη δεν καταλήγει σε κανένα άτοπο, αποκαλύπτει ορισμένα γνωρίσματα του απείρου που ενδέχεται να μας προξενήσουν εντύπωση ως παράδοξα αντίπαλα προς τη διαίσθησή μας, τα οποία δεν ισχύουν όσον αφορά τα πεπερασμένα σύνολα, αλλά συνιστούν αναπόφευκτες συνέπειες της περιγραφής που ορίζει ότι το πεπερασμένο διάστημα ΑΒ απαρτίζεται από άπειρα μικρότερα διαστήματα.
Υπάρχει μια άπειρη ακολουθία φυσικών αριθμών: 1,2, 3... Στη «Διχοτομία» η ακολουθία των διαστημάτων που απαιτείται να διανυθούν μπορεί να τεθεί σε απόλυτη αντιστοιχία με την ακολουθία των φυσικών αριθμών. Το πρώτο διάστημα, το ΑΑ, (το ήμισυ της απόστασης από το Α στο Β) αντιστοιχεί στον αριθμό 1, το δεύτερο διάστημα Α1 Α2 (το ήμισυ της απόστασης από το Α, στο Β) αντιστοιχεί στον φυσικό αριθμό 2 κ.ο.κ. Για κάθε διάστημα υπάρχει ένας φυσικός αριθμός και για κάθε φυσικό αριθμό υπάρχει ένα διάστημα. Όσους φυσικούς αριθμούς και αν μετρήσουμε, πάντοτε θα υπάρχουν και άλλοι· αντίστοιχα, όσα διαστήματα και αν διανύσουμε, πάντοτε θα υπάρχουν και άλλα. Δεν υφίσταται κανένας έσχατος αριθμός και κανένα τελικό διάστημα. Αν η μέτρηση 1,2...κ. ο. κ. συνιστά πράξη αρίθμησης, τότε δεν υφίσταται καμία τελική πράξη αρίθμησης που να εξαντλεί τους φυσικούς αριθμούς. Παρόμοια, καμία διάνυ- ση διαστήματος δεν συνιστά οριστική διάνυση του διαστήματος ΑΒ. Είναι αδύνατο να διανύσουμε τη μια ή την άλλη ακολουθία διασχίζοντας ένα προς ένα τα επιμέρους μέλη της.
Επιπλέον, σε ορισμένες περιπτώσεις το άθροισμα μιας άπειρης ακολουθίας αριθμών αποδεικνύεται πεπερασμένο. Συγκεκριμένα, ας εξετάσουμε την ακολουθία που προκύπτει από τη Διχοτομία 1/2,1/4,1/8..., και ας ονομάσουμε αυτή την ακολουθία Τ. Πρόκειται για άπειρη ακολουθία, καθώς περιέχει άπειρο αριθμό όρων. Οι όροι αυτοί αντιστοιχούν στα μήκη των διαστημάτων που απαιτείται να διανυθούν για να διανυθεί το στάδιο. Ας ορίσουμε το σύνολο των ν πρώτων όρων της ακολουθίας Τ ως το νιοστό μερικό σύνολο του Τ και αυτό το νιοστό μερικό σύνολο του Τ ας το ονομάσουμε Sv. Τότε θα είναι S,=l/2, S2=3/4 κ.ο.κ. Ας θεωρήσουμε ότι το S είναι η ακολουθία S,, S2, S3... Οι όροι του S αντιστοιχούν στη συνολική απόσταση που διανύεται ύστερα από κάθε κίνηση: το 1/2 του σταδίου διανύεται μετά την πρώτη κίνηση, τα 3/4 μετά τη δεύτερη κ.ο.κ. Δεν υπάρχει κανένας τελικός όρος του Τ ή (συνεπώς) του S. Καθώς όλοι οι όροι του Τ είναι μεγαλύτεροι του μηδενός, όσο αυξάνεται το ν εξακολουθεί να αυξάνεται και το Sv. Εφόσον, όμως, κάθε όρος του Τ αποτελεί το ήμισυ μόνο του αμέσως προηγούμενου, το μέτρο στο οποίο αυξάνεται κάθε φορά το Sv αποτελεί το ήμισυ του μέτρου στο οποίο αυξήθηκε την αμέσως προηγούμενη στιγμή. Πράγματι, όλα τα μερικά αθροίσματα είναι μικρότερα της μονάδας. Μια ακριβώς παρόμοια κατάσταση περιγράφει ο Ζήνωνας. Όσο μεγάλο αριθμό διαστημάτων και αν διανύσουμε, δεν έχουμε ακόμη φτάσει στο σημείο τερματισμού (αυτό σημαίνει ότι για κάθε ν ισχύει Sv<l). Επίσης, όσο το ν αυξάνεται, το Sv πλησιάζει τη μονάδα στον επιθυμητό βαθμό (υπό την έννοια ακριβώς ότι για κάθε χ, όσο μικρό και αν είναι αυτό, υπάρχει ένα ψ ώστε να ικανοποιείται η σχέση l-x<S\p. Υπό τις συνθήκες αυτές, οι μαθηματικοί ορίζουν τη μονάδα ως το όριο του Sv όσο το ν πλησιάζει στο άπειρο. Αυτό ακριβώς σημαίνει ότι όσο το ν μεγαλώνει όλο και περισσότερο (ή όσο το ν πλησιάζει στο άπειρο), το Sv πλησιάζει τη μονάδα στον επιθυμητό βαθμό. Αυτό δεν συνεπάγεται ότι το ν φτάνει ποτέ το άπειρο ή ότι το Sv φτάνει ποτέ τη μονάδα, και, συνεπώς, δεν απαιτείται να μιλούμε για εκτέλεση μιας άπειρης ακολουθίας πράξεων.
Η παραπάνω περιγραφή έχει άμεση εφαρμογή στην κίνηση κατά μήκος του σταδίου: όσο μεγάλο αριθμό διαστημάτων και αν διατρέξουμε, δεν φτάνουμε στο σημείο τερματισμού. Από τη στιγμή, όμως, που τα μερικά αθροίσματα αντιστοιχούν στη συνολική απόσταση που καλύπτεται αφού διανύσουμε κάθε διαδοχικό διάστημα, το όριο των μερικών αθροισμάτων αντιστοιχεί προς τη συνολική απόσταση που πρέπει να διανυθεί, το συνολικό δηλαδή μήκος του σταδίου. Όσο περισσότερα διαστήματα διανύουμε, τόσο προσεγγίζουμε το σημείο τερματισμού. Προσεγγίζουμε όσο επιθυμούμε το σημείο τερματισμού υπό την έννοια ότι, για κάθε δεδομένη απόσταση από το σημείο αυτό - δεν έχει σημασία πόσο μικρή είναι αυτή η απόσταση - υπάρχει ένας ορισμένος αριθμός διαστημάτων τέτοιος, ώστε αφού τα διανύσουμε, να βρισκόμαστε σε απόσταση μικρότερη από τη δεδομένη απέναντι στο σημείο τερματισμού, ακόμη και αν δεν υπάρχει κανένα διάστημα το οποίο αφού το διανύσουμε να φτάσουμε στο σημείο τερματισμού.
Ας επιστρέψουμε στην τρίτη προκείμενη. Η ορθότητα ίου ισχυρισμού του Ζήνωνα ότι είναι αδύνατο να διανύσουμε έναν άπειρο αριθμό διαστημάτων έγκειται στη διαπίστωση ότι είναι αδύνατο να διανύσουμε άπειρα διαστήματα ένα προς ένα. Στην άπειρη ακολουθία διαστημάτων δεν υπάρχει ένα τελικό διάστημα. Με άλλα λόγια, στην άπειρη ακολουθία δεν υπάρχει κανένα διάστημα του οποίου η διάνυση να ολοκληρώνει τη διάνυση του σταδίου. Αυτό, όμως, δεν συνεπάγεται ότι δεν μπορούμε σε καμία περίπτωση να διασχίσουμε το στάδιο. Η ψευδαίσθηση ότι αδυνατούμε να το διανύσουμε προέρχεται από την τάση μας να σκεφτόμαστε με όρους του πεπερασμένου. Αν απαιτούνται 100 βήματα για να διατρέξουμε το στάδιο, τότε η διάνυση του σταδίου προϋποθέτει τη διάνυση και των 100 βημάτων. Η διάνυση του σταδίου ολοκληρώνεται με τη διάνυση και του εκατοστού βήματος. Προσδοκούμε, επομένως, ότι αν διασχίζοντας το στάδιο διασχίζουμε μια άπειρη σειρά διαστημάτων, τότε η διαδρομή ολοκληρώνεται με τη διάνυση και του τελικού διαστήματος. Καθώς, όμως, τελικό διάστημα δεν υπάρχει, φαίνεται να προκύπτει πως αδυνατούμε να διανύσουμε το στάδιο. Κατά παρόμοιο τρόπο, η διαδρομή 100 βημάτων ολοκληρώνεται με τη διάνυση και του εκατοστού βήματος, με αποτέλεσμα να προσδοκούμε ότι η διάνυση μιας άπειρης σειράς διαστημάτων ολοκληρώνεται όταν διανύουμε και το τελευταίο από τα άπειρα διαστήματα. Εφόσον, όμως, δεν είμαστε σε θέση να εκτελέσουμε άπειρες πράξεις μία προς μία, εύλογα συνάγεται το συμπέρασμα ότι δεν μπορούμε να διασχίσουμε το στάδιο.
Συμπεράσματα, ωστόσο, αυτού του τύπου δεν προκύπτουν. Στο παράδειγμα που εξετάζουμε, το στάδιο διανύεται με την ολοκλήρωση 100 βημάτων. Από τη στιγμή που το στάδιο μπορεί να ορισθεί ως μια άπειρη σειρά διαστημάτων, η διάνυσή του επιβάλλει να διανυθεί το σύνολο των διαστημάτων. Κατά συνέπεια, αφού διανύσουμε το στάδιο με την ολοκλήρωση 100 βημάτων, έχουμε δια- νύσει την άπειρη σειρά των διαστημάτων. Πρόκειται για απλό συμπέρασμα που απορρέει από τη Ζηνώνεια περιγραφή της κίνησης. Δεν υποδηλώνει, ωστόσο, ότι διανύσαμε το (ανύπαρκτο) τελικό διάστημα. Με άλλα λόγια: για να εκτελέσουμε μια πεπερασμένη ή άπειρη σειρά κινήσεων, πρέπει να εκτελέσουμε όλες τις κινήσεις. (Όταν φτάνουμε στο σημείο τερματισμού, έχουμε διανύσει την απόσταση των 100 βημάτων και έχουμε διανύσει άπειρα διαστήματα). Ενώ, όμως, η ολοκλήρωση μιας πεπερασμένης σειράς κινήσεων σημαίνει ότι εκτελέ- σθηκε και η τελική κίνηση (το εκατοστό βήμα), δεν ισχύει το ίδιο στην περίπτωση της άπειρης σειράς. Αυτό σημαίνει ότι είναι αδύνατο να εκτελέσουμε μια άπειρη σειρά κινήσεων εκτελώντας αυτές τις κινήσεις μία προς μία. Ίσως, όμως, είναι δυνατό αν εκτελέσουμε τις κινήσεις με κάποιον άλλον τρόπο. Επομένως, η προκείμενη (3) ισχύει για τις περιπτώσεις στις οποίες διανύουμε τα άπειρα διαστήματα ένα προς ένα αλλά όχι απαραίτητα για περιπτώσεις στις οποίες διανύουμε τα άπειρα διαστήματα με άλλους τρόπους. Στο παράδειγμά μας, διανύουμε την άπειρη ακολουθία διαστημάτων διανύοντας την απόσταση των 100 βημάτων άρα η προκείμενη (3) δεν ισχύει.
Η «Διχοτομία» αποτυγχάνει. Επιχειρεί να αποδείξει ότι η κοινή θεώρηση της κίνησης καταλήγει σε αντίφαση: έχουμε την πεποίθηση ότι μπορούμε να διανύ- σουμε το στάδιο αλλά από τις προκείμενες (1) (2) (3) έπεται το αντίθετο. Η κοινή θεώρηση της κίνησης μας υποχρεώνει να αποδεχθούμε τις προκείμενες (1), (2). Η ευλογοφάνεια, ωστόσο, της προκείμενης (3) βασίζεται σε έναν συγκεκριμένο τρόπο εκτέλεσης απείρων κινήσεων. Αν υπάρχουν άλλοι τρόποι, και, συγκεκριμένα, αν υπάρχει κάποιος τρόπος που προκύπτει από τη διάνυση του σταδίου με έναν πεπερασμένο αριθμό (πεπερασμένων) βημάτων, δεν συντρέχει λόγος να αποδεχθούμε την άποψη του Ζήνωνα. Πράγματι, υπάρχει τέτοιος τρόπος. Μπορούμε αποδεχόμενοι την Ζηνώνεια ανάλυση της κίνησης στις προκείμενες (1) και (2) να δείξουμε ότι η ανάλυση αυτή όχι μόνο δεν αποκλείει την ύπαρξη της κίνησης αλλά είναι απόλυτα συμβατή με αυτήν. (Το ευπρόσδεκτο αυτό συμπέρασμα ισχύει). Όταν διανύουμε το στάδιο με 100 βήματα, ολοκληρώνουμε τη διάνυση του πρώτου διαστήματος ύστερα από 50 κατά τη Ζηνώνεια εκδοχή βήματα (βλ. προκείμενη 1). Ύστερα από 25 ακόμη βήματα διανύουμε το δεύτερο κατά τη Ζηνώνεια εκδοχή διάστημα. Με 13 ακόμη βήματα ολοκληρώνουμε τη διάνυση και του τρίτου διαστήματος. (Έχουμε καλύψει απόσταση 88 μέτρων και το τρίτο διάστημα έχει ως τελικό όριο τα 87,5 μέτρα). Παρόμοια, θα έχουμε διανύσει το 4ο, 5ο, και 6ο διάστημα από τη στιγμή που θα έχουμε ολοκληρώσει 94,97 και 99 βήματα αντίστοιχα. Όταν θα έχουμε ολοκληρώσει τα 100 βήματα, θα έχουμε διανύσει όλα τα εναπομείναντα διαστήματα - έναν άπειρο δηλαδή αριθμό διαστημάτων. Η διάνυση άπειρων διαστημάτων είναι εφικτή με αυτόν τον τρόπο που απαιτείται για την ανασκευή της «Διχοτομίας». Αντίθετα, μάλιστα, από την προηγούμενη απόπειρα εξεύρεσης λύσης, η οποία χρέωσε στον Ζήνωνα σκέψεις που ο ίδιος δεν έκανε, η λύση που προτείνουμε δεν προσφέρει απλώς μια εναλλακτική περιγραφή της κίνησης που δεν οδηγεί σε παράδοξα. Αντίθετα, αποδεικνύει ότι η ανάλυση της κίνησης από τον Ζήνωνα όχι μόνο δεν συνεπάγεται ότι η κίνηση είναι αδύνατη αλλά και οδηγεί σε συμπεράσματα συμβατά με την ύπαρξη της κίνησης - συμπεράσματα που θα ήταν ιδιαίτερα προβληματικά αν δεν προέκυπταν από τις δύο πρώτες προκείμενες του Ζήνωνα.
Ο ΑΧΙΛΛΕΑΣ
Παραθέτουμε την ακόλουθη διεξοδική ερμηνεία του «Αχιλλέα»:
«Ο Αχιλλέας ποτέ δεν θα φτάσει τη χελώνα ακόμη και αν τρέχει ταχύτερα από αυτήν. Τη στιγμή που ο Αχιλλέας φτάνει στο σημείο (Α) από όπου ξεκίνησε η χελώνα, αυτή έχοντας καλύψει κάποια απόσταση, έστω και μικρή, θα έχει φτάσει σε ένα νέο σημείο (Α,). Τη στιγμή που ο Αχιλλέας φτάνει στο σημείο ΑΡ η χελώνα θα έχει μετακινηθεί σε ένα άλλο σημείο Α2 κ.ο.κ. Κάθε φορά που ο Αχιλλέας φτάνει στο σημείο στο οποίο είχε φτάσει η χελώνα, η χελώνα δεν βρίσκεται πια εκεί- η χελώνα πάντοτε προπορεύεται με αποτέλεσμα ο Αχιλλέας ποτέ να μην την φτάνει».
Όπως σημείωσα παραπάνω, το παράδοξο αυτό βασίζεται στους προσδιορισμούς άεί και ουδέποτε, και όχι στις ιδιότητες των άπειρων σειρών, παρόλο που σύμφωνα με την περιγραφή του Ζήνωνα ο αγώνας δρόμου συνίσταται στη διάνυση απείρως πολλών διαστημάτων. Το παράδοξο διατυπώνεται από τη σκοπιά του Αχιλλέα. Ο Αχιλλέας ποτέ δεν θα διανύσει όλες τις επιμέρους αποστάσεις που απαιτείται να διανυθούν για να ολοκληρώσει τη διαδρομή, με την έννοια ότι, όσες επιμέρους αποστάσεις και αν έχει διανύσει σε κάθε στιγμή, πάντοτε θα είναι περισσότερες αυτές που απομένουν να διανυθούν. Υπό τις συνθήκες αυτές, δεν ωφελεί να επισημάνουμε ότι ο Αχιλλέας πλησιάζει τη χελώνα στο μέτρο που επιθυμεί (με την έννοια που ορίσαμε στη σ. 229) ή ότι θα φτάσει τη χελώνα αφού διατρέξει μια απόσταση ίση με τον λόγο ΧΨ/ (Ψ-Ζ) και αφού τρέξει για χρόνο ίσο με τον λόγο X/ (Ψ-Ζ), όπου X είναι το αρχικό αφε- τηριακό σημείο, Ψ είναι η ταχύτητα του Αχιλλέα και Ζ η ταχύτητα της χελώνας. Το πρόβλημα δεν έγκειται στο γεγονός ότι δεν υπάρχει καμία στιγμή κατά την οποία ο Αχιλλέας θα φτάσει τη χελώνα ή κανένα σημείο στο οποίο τη φτάνει, αλλά στη διαπίστωση ότι η άφιξη στο σημείο αυτό (και στη συγκεκριμένη στιγμή) προϋποθέτει ότι ο δρομέας θα επιτύχει κάτι ανέφικτο.
Σύμφωνα με μια εύλογη ερμηνεία των προσδιορισμών άεί και ουδέποτε η φράση «η χελώνα πάντοτε προπορεύεται» σημαίνει ότι «η χελώνα προπορεύεται σε κάθε χρονική στιγμή» και η φράση «ο Αχιλλέας ποτέ δεν φτάνει τη χελώνα» σημαίνει ότι «δεν υπάρχει καμία στιγμή κατά την οποία ο Αχιλλέας φτάνει τη χελώνα». Το παράδοξο, ωστόσο, δεν δικαιώνει αυτούς τους ισχυρισμούς αλλά μας καλεί να εκλάβουμε τις δύο προτάσεις διαφορετικά: η πρόταση «η χελώνα πάντοτε προπορεύεται» ισοδυναμεί με τον ισχυρισμό ότι «σε κάθε χρονική στιγμή κατά τη διάρκεια του αγώνα (δηλαδή ενώ ο Αχιλλέας προσπαθεί να φτάσει τη χελώνα) η χελώνα προπορεύεται»· η πρόταση, επίσης, «ο Αχιλλέας ποτέ δεν φτάνει τη χελώνα» ισοδυναμεί με τον ισχυρισμό ότι «δεν υπάρχει καμία χρονική στιγμή όσο διαρκεί ο αγώνας κατά την οποία ο Αχιλλέας φτάνει τη χελώνα».
Γίνεται σαφές ότι η διατύπωση «η χελώνα πάντοτε προπορεύεται ενώ ο Αχιλλέας προσπαθεί να τη φτάσει» δεν συνεπάγεται ότι η χελώνα πάντοτε προπορεύεται· και όμως, ό,τι αποδεικνύει το παράδοξο είναι ο πρώτος ανώδυνος ισχυρισμός· με το παράδοξο αυτό, ωστόσο, ο στοχαστής αποσκοπεί στην απόδειξη του δεύτερου ισχυρισμού· ο δεύτερος ισχυρισμός, και όχι ο πρώτος, είναι που έρχεται σε αντίθεση με την κοινή θεώρηση της κίνησης. Θα νιώθαμε κατάπληξη αν διαβάζαμε ότι ο Αχιλλέας ποτέ και σε καμία περίπτωση δεν θα φτάσει τη χελώνα· θα ήταν πιο ευπρόσδεκτη και πράγματι δεν θα προκαλούσε έκπληξη η ταυτολογική στην ουσία άποψη ότι ο Αχιλλέας δεν φτάνει τη χελώνα σε καμία χρονική στιγμή πριν από τη λήξη του αγώνα, δηλαδή προτού τη φτάσει.
Ο «Αχιλλέας» δεν ισχύει διότι εκμεταλλεύεται την αμφισημία. Επιπλέον, προϋποθέτει μια άπειρη σειρά πράξεων που υπόκειται στην ίδια ανάλυση στην οποία υπόκειται και η σειρά των διαστημάτων που συναντήσαμε στον συλλογισμό της «Διχοτομίας». Η σειρά δεν έχει κανέναν τελικό όρο και δεν μπορεί να ολοκληρωθεί με την εκτέλεση των πράξεων μια προς μια (όπως το παράδοξο παρουσιάζει τον Αχιλλέα να ενεργεί). Σύμφωνα με την προηγούμενη παρουσίασή μας, το εκατοστό μη διαιρετό βήμα που κάνουμε για τη διάνυση του σταδίου μάς τοποθετεί σε μια θέση όπου έχουμε διανύσει πλήρως την άπειρη σειρά διαστημάτων που σύμφωνα με τη «Διχοτομία» πρέπει να διανύσουμε· κάτι παρόμοιο ισχύει και εδώ: όταν ο Αχιλλέας ολοκληρώσει το τελικό μη διαιρετό βήμα, θα έχει διανύσει πλήρως την άπειρη σειρά των διαστημάτων που, όπως δείχνει το παράδοξο, πρέπει να διανύσει. Πρόκειται και πάλι για μια ευπρόσδεκτη κατάσταση που μάλλον ενισχύει παρά υποσκάπτει την κοινή θεώρηση της κίνησης.
ΤΟ ΒΕΛΟΣ (ὀιστός φερομένη)
«Αν καθετί βρίσκεται πάντοτε σε κατάσταση ηρεμίας, όταν καταλαμβάνει χώρο ίσο με τον εαυτό του και αν καθετί που κινείται βρίσκεται πάντα σε ένα «χρονικό παρόν», τότε το κινούμενο βέλος είναι ακίνητο» (Αριστοτέλη, Φυσικά 6. 9 239b5-7 [μτφρ. Δ.Κ.]) [εἰ γάρ ἀεί, φησίν, ἠηρεμεῖ πᾶν [ἤ κινεῖται], ὅταν ᾖ κατά τό ἴσον, ἔστι δ’ ἀεί τό φερόμενον ἐν τῷ νῦν, ἀκίνητον τήν φερομένην εἶναι ὀιστόν].
Το επιχείρημα μπορεί να αναλυθεί ως εξής:
1) Όταν κάτι καταλαμβάνει χώρο ίσο με τον εαυτό του στον χρόνο t, τότε βρίσκεται σε ηρεμία στον χρόνο t.
2) Σε κάθε στιγμή («τώρα») της κίνησής του, το βέλος καταλαμβάνει χώρο ίσο με τον εαυτό του.
3) Σε κάθε στιγμή («τώρα») της κίνησής του, το βέλος βρίσκεται σε ηρεμία (όπως προκύπτει από τις προκείμενες 1 και 2).
4) Το κινούμενο βρίσκεται πάντοτε σε μία χρονική στιγμή· αυτό σημαίνει ότι η συνολική διάρκεια της κίνησής του αποτελείται από επιμέρους στιγμές («τώρα»).
5) Το βέλος, καθ’ όλη τη διάρκεια της κίνησής του, ηρεμεί (όπως προκύπτει από τις προκείμενες 3 και 4).
Ορισμένες από τις παραπάνω προτάσεις χρειάζονται περαιτέρω διευκρίνιση. Η πρώτη πρόταση προσφέρει τον όρο που απαιτείται για να θεωρήσουμε ότι κάτι ηρεμεί· δύσκολα, ωστόσο, γίνεται αντιληπτή η αντίστοιχη άποψη για την κίνηση. Σύμφωνα με την πρώτη πρόταση, όταν κάτι δεν βρίσκεται σε κατάσταση ηρεμίας, όταν δηλαδή κινείται, τότε δεν καταλαμβάνει χώρο ίσο με τον εαυτό του αλλά προφανώς μεγαλύτερο. Αν θεωρήσουμε τον χρόνο t ως στιγμή («χρονικό παρόν»), τότε ο Ζήνωνας ισχυρίζεται ότι τα κινούμενα αντικείμενα «διαστέλλονται», με αποτέλεσμα να αποκλείει το ενδεχόμενο της κίνησης ενός αντικειμένου ως ελαστικού σώματος που εκτείνεται από το Α έως το Β, έπειτα εκτείνεται καλύπτοντας την απόσταση από το Α έως το Δ, και στη συνέχεια επανέρχεται στο αρχικό του μήκος καλύπτοντας την απόσταση από το Γ έως το Δ. (Έτσι, η απόσταση μεταξύ Α και Β ισοδυναμεί με την απόσταση μεταξύ Γ και Δ και είναι μικρότερη από την απόσταση ΑΔ). Αν σε χρονική στιγμή t το ελαστικό σώμα εκτείνεται από το Α έως το Δ, τότε κατά τη χρονική στιγμή t κινείται υπό την έννοια ότι παύει να καταλαμβάνει το διάστημα ΑΒ και καταλαμβάνει το διάστημα ΓΔ. Με γνώμονα την ερμηνεία αυτή, η (3) προκύπτει βάσιμα από τις (1) και (2)· δεν γίνεται, ωστόσο, σαφές γιατί θα έπρεπε ο Ζήνωνας να θεωρεί ότι η κίνηση συνεπάγεται αναπόφευκτα τη διαστολή του κινούμενου σώματος. Μια άλλη δυνατότητα είναι η θεώρηση του χρόνου t ως διαστήματος· στην περίπτωση αυτή ο Ζήνωνας υποστηρίζει ότι αν το X, του οποίου οι διαστάσεις παραμένουν αμετάβλητες, κινείται κατά το διάστημα t καθώς, ενώ καταλάμβανε το διάστημα ΑΒ, καταλαμβάνει τώρα το διάστημα ΓΔ, τότε κατά το διάστημα t, το X καταλαμβάνει το συνολικό διάστημα ΑΔ, το οποίο είναι μεγαλύτερο από το X (από τον χώρο δηλαδή ΑΒ). Αυτό δεν σημαίνει ότι σε οποιαδήποτε στιγμή του t το X καταλαμβάνει το συνολικό διάστημα ΑΔ ή οποιονδήποτε άλλο χώρο με τον οποίο δεν είναι ίσο. Με βάση την ερμηνεία αυτή, (η οποία δύσκολα εξάγεται από το κείμενο) συνάγουμε μια πιο ευλογο- φανή εξήγηση του τι συμβαίνει κατά τη διάρκεια της κίνησης, και ο ισχυρισμός ότι, αν το X καταλαμβάνει διάστημα ΑΒ σε όλη τη διάρκεια του χρόνου t, τότε το X ηρεμεί στον χρόνο t, είναι αληθής. Η μετάβαση, ωστόσο, από την προκεί- μενη (2) στην προκείμενη (3) είναι αδύνατη καθώς οι προκείμενες (2) και (3) αφορούν την κίνηση σε μια στιγμή και όχι σε ένα χρονικό διάστημα.
Έχω προσθέσει τις προκείμενες (2) και (3), οι οποίες δεν περιέχονται στο αριστοτελικό κείμενο αλλά συνιστούν τον πιο εύλογο τρόπο για να ολοκληρωθεί το επιχείρημα. Η μετάβαση από την προκείμενη (4) στην προκείμενη (5) απαιτεί μια επιπλέον προκείμενη που αφορά χρονικά σημεία (και όχι διαστήματα). Στην προκείμενη (4) η φράση εν τφ νϋν μεταφράζεται συνήθως «στο παρόν», δηλαδή «σε μια στιγμή».
Αυτό το παράδοξο γεννά δυσεπίλυτα προβλήματα σχετικά με τη φύση της κίνησης. Θα επιχειρήσω να εκθέσω δύο από αυτά. Στην προκείμενη (1) ο Ζήνωνας υποθέτει ότι ένα πράγμα ενδέχεται να ηρεμεί σε μια στιγμή, κάτι που σύμφωνα με τον Αριστοτέλη είναι αδύνατο. Ο Αριστοτέλης υποστηρίζει ότι η κίνηση συμβαίνει όχι σε ένα σημείο του χρόνου αλλά σε ένα διάστημα χρόνου. Επιπλέον, εφόσον η ηρεμία είναι η απουσία κίνησης, παρατηρείται, επίσης, σε χρονικά διαστήματα. Όσο δυνατό είναι να ηρεμεί κάτι σε μια στιγμή, τόσο δυνατό είναι και να κινείται σε μια στιγμή (Φυσικά 6. 3 234a24-b9). Ο Αριστοτέλης, όμως, σφάλλει όπως αποδείχτηκε όταν τελικά η μαθηματική ανάλυση θεμελιώθηκε στον 19° αιώνα. Πράγματι, δεν έχουμε άδικο όταν κάνουμε λόγο για κίνηση και ηρεμία σε μια στιγμή: «3 ακριβώς λεπτά και 12 δευτερόλεπτα μετά τις 8:00 μ.μ. οδηγούσα με 65 km/h. Έπεσα σε κυκλοφοριακή συμφόρηση από τις 8:10 περίπου έως τις 8:20, με αποτέλεσμα για 15 λεπτά ακριβώς και π δευτερόλεπτα μετά τις 8:00 το αυτοκίνητό μου να μένει ακίνητο». Ακόμη και αν η κύρια σημασία της κίνησης (και της ηρεμίας) προϋποθέτει ένα διάστημα χρόνου στο οποίο συμβαίνει η κίνηση, είναι δυνατό να αναφερθούμε σε κάτι ως κινούμενο ή ακίνητο σε μια στιγμή- δεν εννοούμε ότι το σώμα διανύει οποιαδήποτε απόστάση σε μια στιγμή, αλλά ότι ενδέχεται να έχει ταχύτητα σε μια στιγμή, εφό- σον, όταν η ταχύτητά του είναι μηδενική, τότε βρίσκεται σε ηρεμία, ενώ όταν η ταχύτητά του είναι διάφορη του μηδενός κινείται. Η ταχύτητα σε ένα χρονικό διάστημα ορίζεται ως ο λόγος της απόστασης που καλύπτεται στο εν λόγω διάστημα χρόνου προς το μήκος του χρονικού διαστήματος:
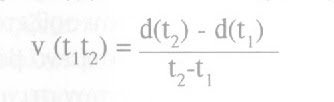
Αντίστοιχα, η ταχύτητα στη στιγμή t ισοδυναμεί με το όριο (κατά τον ίδιο τρόπο που ορίσαμε παραπάνω, σ. 229) του λόγου της απόστασης που διανύε- ται στα χρονικά διαστήματα που περιέχουν το t προς το μήκος αυτών των διαστημάτων που τείνει στο μηδέν. Αν το t, προηγείται του t2 και το χρονικό διάστημα tjt2 περιέχει το t, τότε, η ταχύτητα στον χρόνο t είναι το όριο του λόγου της απόστασης που διανύεται μεταξύ t, και t2 προς το μήκος του χρονικού διαστήματος μεταξύ t, και t2 που τείνει στο μηδέν:

Ακόμη και αν ο Ζήνωνας δέχεται τα παραπάνω, η προκείμενη (4) γεννά ένα ακόμη πρόβλημα. Σε διαφορετικές στιγμές το κινούμενο βέλος βρίσκεται σε διαφορετικά σημεία της τροχιάς του- πώς, όμως, κινείται από το ένα σημείο στο άλλο; Ο Αριστοτέλης υποστηρίζει ότι το συμπέρασμα του Ζήνωνα απορρέει από την υπόθεση ότι ο χρόνος αποτελείται από στιγμές- αν η υπόθεση δεν ευσταθεί, το συμπέρασμα απορρίπτεται (Αριστοτέλη Φυσικά 6. 9 239b30-33) [συμβαίνει δέ παρά τό λαμβάνειν τον χρόνον συγκεΐσθαι εκ των νϋν μή δίδομένον γάρ τούτον ούκ έσται ό συλλογισμός]. Το πρόβλημα κατά τον Αριστοτέλη έχει ως εξής: αν ο χρόνος είναι ζήτημα ατομικής αίσθησης, τότε υφί- στανται διαδοχικές χρονικές στιγμές. Αν κάτι κινείται, καταλαμβάνει σε διαφορετικές χρονικές στιγμές διαφορετικούς χώρους. Αν οι χρόνοι t, και t2 συνι- στούν διαδοχικές χρονικές στιγμές, αυτό που κινείται στο χρονικό διάστημα t,t2 καταλαμβάνει διαφορετικούς χώρους d (t,) και d (t2) στα χρονικά διαστήματα t, και t2 αντίστοιχα. Πότε, όμως, κινείται από το d (t,) στο d (t2); Απάντηση δεν μπορεί να δοθεί, καθώς για να πραγματοποιηθεί η κίνηση δεν υπάρχει καθόλου χρόνος, καμία χρονική στιγμή μεταξύ t, και t2.
Ο Αριστοτέλης επιλύει το παράδοξο απορρίπτοντας την υπόθεση του Ζήνωνα ότι ο χρόνος αποτελείται από στιγμές. Αν ο χρόνος είναι συνεχής, δεν υφί- στανται διαδοχικές στιγμές. Μεταξύ δύο οποιωνδήποτε στιγμών t, και t2 υπάρχει μια στιγμή t3. Καθώς και η κίνηση, επίσης, είναι συνεχής, υφίσταται απόλυτη αντιστοιχία ανάμεσα στις στιγμές της κίνησης του βέλους και στις θέσεις που αυτό καταλαμβάνει κατά την κίνησή του. Το βέλος κινείται από το σημείο d (t,) στο σημείο d (t2) στο διάστημα που ορίζεται από το t, και το t2· για κάθε σημείο d (t3) που καταλαμβάνει το κινούμενο βέλος ανάμεσα στα σημεία d (t,) και d (t2) υπάρχει μια στιγμή t3 μεταξύ των στιγμών t, και t2 κατά την οποία το βέλος βρίσκεται στο σημείο d (t3)· για κάθε, επίσης, στιγμή t3 μεταξύ των στιγμών t, και t2, υπάρχει στην πορεία του βέλους και μεταξύ των σημείων d (t,) και d (t2) ένα σημείο d (t3) που καταλαμβάνει το βέλος τη στιγμή t3. Έτσι, η κίνηση δεν συνεπάγεται στιγμικά άλματα από το ένα σημείο του χώρου στο άλλο ή από τη μια στιγμή στην άλλη.
Η παραπάνω απάντηση δεν είναι εντελώς ικανοποιητική. Αν ο χώρος, ο χρόνος και η κίνηση είναι συνεχή μεγέθη, τότε δεν αποτελούνται, όπως αποδεικνύ- ει το απ. Β1 (σ. 217-218), από ελάχιστες μονάδες με συγκεκριμένο μέγεθος. Ούτε αποτελούνται από μονάδες μηδενικού μεγέθους, όπως υποθέτει το απ. Β2 (σ. 217). Κατά τον Αριστοτέλη, αποτελούνται από διαστήματα, και όχι από σημεία· σύμφωνα με τα παραπάνω, ο Αριστοτέλης θεωρεί ότι κίνηση είναι η διάνυση μιας ορισμένης απόστασης σε ένα χρονικό διάστημα. Η επίλυση, ωστόσο, του προηγούμενου προβλήματος, σύμφωνα με την οποία υπάρχει κίνηση σε μια χρονική στιγμή, υποδηλώνει ότι υπό μια έννοια τα συνεχή μεγέθη του χρόνου, του χώρου και της κίνησης αποτελούνται από σημεία. Μπορούμε με συνέπεια να κάνουμε λόγο όχι μόνο για ταχύτητα σε μια στιγμή t αλλά και για κίνηση κατά το χρονικό διάστημα από το ^ έως το t2 σαν να πρόκειται για το άθροισμα των κινήσεων που συντελούνται σε κάθε στιγμή μεταξύ t, και t2. Αν γνωρίζουμε ποια είναι η τιμή της ταχύτητας σε κάθε σημείο, μπορούμε να προσδιορίσουμε την κίνηση επί του συνολικού διαστήματος μέσω του ορισμένου ολοκληρώματος της ταχύτητας στο διάστημα από το t, έως το t2.
Στο σημείο αυτό, ωστόσο, προκύπτει ένα πρόβλημα παρόμοιο με το αρχικό. Καθώς η κίνηση προϋποθέτει ότι ένα σώμα βρίσκεται σε διαφορετικά σημεία σε διαφορετικές στιγμές, παραμένει το εξής πρόβλημα: πώς το βέλος μεταβαίνει από ένα σημείο σε ένα άλλο ή πώς μεταβαίνει από τη μια στιγμή στην άλλη. Το βέλος δεν κινείται με άλματα από ένα χωρικό ή χρονικό σημείο στο επόμενο, διότι, καθώς το διάστημα είναι συνεχές, κανένα σημείο του δεν νοείται ως επόμενο κάποιου προηγούμενου. Πρέπει όμως να μεταβεί τόσο από το σημείο d (t,) στο σημείο d (t2) διανύοντας όλα τα ενδιάμεσα σημεία όσο και από το σημείο t, στο t2 περνώντας από όλα τα ενδιάμεσα σημεία.
Η μετάβαση του βέλους από το ένα σημείο του χώρου στο άλλο και από τη μια στιγμή στην άλλη εξηγούνται ως εξής: Το βέλος για να κινηθεί συνεχώς από το σημείο d (t,) στο σημείο d (t2) κατά το χρονικό διάστημα μεταξύ της στιγμής t, και της στιγμής t2 πρέπει συνεχώς να καταλαμβάνει διαφορετικές θέσεις από το d (t,) έως το d (t2) σε κάθε διαφορετική στιγμή του διαστήματος t,-t2, χωρίς να ηρεμεί και χωρίς να αλλάζει τη φορά της κίνησής του. Παρόμοια, όταν το βέλος κινείται σε όλη τη διάρκεια του διαστήματος από τη στιγμή t, έως τη στιγμή t2, κινείται στη διάρκεια όλων των υποδιαστημάτων από τη στιγμή t, έως τη στιγμή t2. Η κίνηση ορίζεται αυστηρά σε ένα διάστημα του χώρου και του χρόνου διαστημάτων και μόνο δευτερευόντως σε ένα σημείο του χώρου ή σε μια στιγμή. Συνεπώς, αν το βέλος κινείται συνεχώς από το σημείο d (t,) έως το σημείο d (t2), τότε διασχίζει όλα τα ενδιάμεσα σημεία. Κατά τον ίδιο τρόπο, αν πραγματοποιεί συνεχή κίνηση κατά το χρονικό διάστημα από τη στιγμή t, έως τη στιγμή ΐ2, τότε περνά από όλες τις ενδιάμεσες χρονικές στιγμές.
Όσον αφορά τα σημεία του χώρου και τις στιγμές, η απάντηση είναι ότι το βέλος κινείται (έχει δηλαδή ταχύτητα διάφορη του μηδενός) όταν βρίσκεται σε ένα σημείο d(t), με την έννοια ότι διανύει ένα ορισμένο διάστημα του χώρου που περιέχει το d(t). Κινείται, επίσης, κατά τη στιγμή t, με την έννοια ότι κινείται στη διάρκεια ενός χρονικού διαστήματος που περιέχει τη στιγμή t. Η απάντηση στο ερώτημα πώς το βέλος μεταβαίνει από ένα σημείο του χώρου σε ένα άλλο ή περνά από μια στιγμή σε μια άλλη κατά την κίνησή του, προκύπτει από τη θέση ότι αυτή ακριβώς η μετάβαση συνιστά την κίνηση του βέλους.
ΤΑ ΠΑΡΑΔΟΞΑ: ΣΥΜΠΕΡΑΣΜΑ
Ορισμένα από τα παράδοξα του Ζήνωνα τα επέλεξα λόγιο της ιστορικής τους αξίας και της φιλοσοφικής τους σημασίας- άλλα επιλέχθηκαν επειδή προδίδουν χαρακτηριστικά γνωρίσματα του τρόπου σκέψης του στοχαστή. Σώζονται και άλλα παράδοξα, το καθένα από τα οποία εμφανίζει τη δική του πολυ- πλοκότητα. Ήδη, όμως, παρουσιάσαμε μεγάλο μέρος του υλικού και, συνεπώς, μπορούμε να συναγάγουμε τα συμπεράσματα της επισκόπησής μας.
Τα επιχειρήματα που εξετάσαμε στο παρόν κεφάλαιο στρέφονται κατά της πολλαπλότητας και της κίνησης. Ένα άλλο επιχείρημα απορρίπτει την αξιοπιστία της αίσθησης της ακοής, ενώ ένα τρίτο στρέφεται εναντίον της άποψης ότι τα πράγματα έχουν θέσεις. Εφόσον οι άνθρωποι της καθημερινότητας (αντίθετα, ενδεχομένως, από ορισμένους φιλοσόφους) αποδέχονται την πολλαπλότητα και την κίνηση, βασιζόμενοι (σε κάποιον τουλάχιστον βαθμό) στη μαρτυρία των αισθήσεων και θεωρώντας ότι ορισμένα πράγματα έχουν θέσεις, συμπεραίνουμε ότι δικαιούμαστε να πιστεύουμε πως ο Ζήνωνας στράφηκε με τα παράδοξά του εναντίον των καθιερωμένων κοσμοαντιλήψεων, και αυτό αποτέλεσε το κριτήριο για τον τρόπο με τον οποίο παρουσιάσαμε τα παράδοξα του στοχαστή. Η μαρτυρία του Πλάτωνα ότι το βιβλίο του Ζήνωνα «συνιστά υπεράσπιση της παρμενίδειας θεωρίας έναντι εκείνων οι οποίοι επιχειρούν να τη διακωμωδήσουν ισχυριζόμενοι ότι, αν υφίσταται το "Εν, τότε η θεωρία καταλήγει σε κωμικά αποτελέσματα και υποπίπτει σε αντιφάσεις» (Παρμενίδης 128c-d), δεν έρχεται σε αντίθεση με την άποψη που πρέσβευε ο Ζήνωνας. Οι καθημερινοί και χωρίς φιλοσοφικές ανησυχίες άνθρωποι που άκουσαν το ποίημα του Παρμενίδη, θα διακωμωδούσαν τις απόψεις του Ζήνωνα κατά τον ίδιο τρόπο και για τους ίδιους ακριβώς λόγους.
Υπήρξε εποχή κατά την οποία οι μελετητές πρέσβευαν την ευρέως αποδεκτή άποψη ότι ο Ζήνωνας συνέθεσε τα παράδοξό του έχοντας υπόψη του συγκεκριμένους φιλοσόφους και μαθηματικούς και κατά κύριο λόγο τους Πυθαγορείους. Άλλοι μελετητές υποστηρίζουν ότι ο Ζήνωνας επιχείρησε να ανασκευ- άσει κάθε πιθανή θεωρία για τον χώρο, τον χρόνο και την κίνηση και θεωρούν ότι η επιδίωξη του στοχαστή δεν ήταν να απορρίψει τις ιδέες των ανθρώπων της καθημερινότητας ή συγκεκριμένων φιλοσόφων αλλά να ορθώσει εμπόδια σε κάθε πιθανή θεωρία σχετικά με τη φύση του χώρου, του χρόνου, και της κίνησης. Για παράδειγμα, η «Διχοτομία» και ο «Αχιλλέας» στρέφονται κατά των θεωριών που πρεσβεύουν ότι ο χώρος και ο χρόνος επιδέχονται άπειρη διαίρεση. Το «Βέλος» αντιτίθεται στις θεωρίες που πρεσβεύουν ότι ο χώρος και ο χρόνος δεν είναι απείρως διαιρετά μεγέθη. Οι μαρτυρίες, ωστόσο, για τις απόψεις αυτές είναι από πενιχρές έως ανύπαρκτες και θεωρούνται παρωχημένες. Η αίσθηση που απομένει είναι ότι ο Ζήνωνας στρέφεται κατά του κοινού νου, που δεν αποτελεί αποκλειστικό προνόμιο των φιλοσόφων.
Η μαρτυρία του Πλάτωνα για τον Ζήνωνα εξακολουθεί να αποτελεί ικανοποιητική ερμηνεία της σκέψης του στοχαστή. Δεν συντρέχει κανένας λόγος ώστε να θεωρήσουμε ότι είναι αμφίβολη η μαρτυρία πως σκοπός του Ζήνωνα ήταν να υπερασπισθεί, με τον τρόπο που είδαμε, τον Παρμενίδη (σσ. 211-214,224 και 216 σημ. 12). Και αν ακόμη ο Πλάτωνας αναφέρει ότι όλα τα επιχειρήματα του Ζήνωνα στρέφονται κατά της πολλαπλότητας, αυτό δεν σημαίνει υποχρεωτικά ότι ο Πλάτωνας δεν γνώριζε ορισμένα από τα σωζόμενα παράδοξα, μεταξύ των οποίων και εκείνα που απορρίπτουν την κίνηση. Προτείνω την εύλογη σκέψη ότι ο Πλάτωνας χρησιμοποίησε τη φράση «τα πάντα είναι ένα» ως έμβλημα της συνολικής φιλοσοφίας των Ελεατών. Συνεπώς, ο ισχυρισμός ότι ο Ζήνωνας επιχειρηματολόγησε κατά των υποστηρικτών της πολλαπλότητας απλώς ανα- δεικνύεται σε μέσο έκφρασης της αλήθειας: Τα επιχειρήματα του Ζήνωνα στράφηκαν κατά των απόψεων που έρχονταν σε αντίθεση με τις αρχές του Ελεατι- σμού. Αν αυτό ισχύει, τότε όλα τα σωζόμενα παράδοξα είναι πιθανό να προέρχονται από το βιβλίο που μνημονεύει ο Πλάτωνας.
----------------------
Όσον αφορά τις επιφυλάξεις απέναντι σε αυτές τις χρονολογήσεις, βλ. Mansfeld [32] 64-68.
 ΕΠΕΙΣΟΔΙΟΝ Δ΄
ΕΠΕΙΣΟΔΙΟΝ Δ΄