ΦΙΛΟΣΟΦΙΑ: Πρώιμες σύγχρονες αντιλήψεις ανάλυσης

Πρώιμες σύγχρονες αντιλήψεις ανάλυσης

1. Εισαγωγή
2. Ντεκάρτ και Αναλυτική Γεωμετρία
3. Βρετανικός Εμπειρισμός
4. Λάιμπνιτς
5. Καντ
6. Ινδική Αναλυτική Φιλοσοφία
7. Dai Zhen και Κινεζική Φιλολογική Ανάλυση
8. Συμπέρασμα

1. Εισαγωγή

Αυτό το συμπλήρωμα σκιαγραφεί πώς προέκυψε μια αναγωγική μορφή ανάλυσης στην ανάπτυξη της αναλυτικής γεωμετρίας από τον Ντεκάρτ και επεξεργάζεται τον τρόπο με τον οποίο οι αποσυνθετικές αντιλήψεις της ανάλυσης ήρθαν στο προσκήνιο στην ευρωπαϊκή φιλοσοφία κατά την πρώιμη σύγχρονη περίοδο. Σε αντίθεση με αυτές τις εξελίξεις στην Ευρώπη είναι η εμφάνιση αυτού που δικαίως μπορεί να περιγραφεί ως μια μορφή αναλυτικής φιλοσοφίας στην Ινδία, αρκετούς αιώνες πριν από την εμφάνισή της στην Ευρώπη. Μια σύντομη σύγκριση γίνεται επίσης με την παράδοση της φιλολογικής ανάλυσης στην Κίνα, η οποία έφτασε στο απόγειο του έργου του Dai Zhen.

2. Ντεκάρτ και Αναλυτική Γεωμετρία

Σε ένα διάσημο απόσπασμα των απαντήσεών του στις αντιρρήσεις του Μερσέν για τους Διαλογισμούς, συζητώντας τη διάκριση μεταξύ ανάλυσης και σύνθεσης, ο Ντεκάρτ παρατηρεί ότι «η ανάλυση είναι η καλύτερη και πιο αληθινή μέθοδος διδασκαλίας, και ήταν μόνο αυτή η μέθοδος που χρησιμοποίησα στους Διαλογισμούς μου» (PW, II, 111). Σύμφωνα με τον Ντεκάρτ, είναι η ανάλυση και όχι η σύνθεση που έχει τη μεγαλύτερη αξία, αφού δείχνει «πώς ανακαλύφθηκε το εν λόγω πράγμα» και κατηγορεί τους αρχαίους γεωμέτρες ότι κρατούσαν τις τεχνικές της ανάλυσης για τον εαυτό τους «σαν ιερό μυστήριο» (ό.π.· βλ. PW, I, 17). Τα Στοιχεία του Ευκλείδη είναι πράγματι διατυπωμένα σε «συνθετική» μορφή, αλλά είναι άδικο να προτείνουμε ότι κάποιος που δούλεψε το κείμενο δεν θα αποκτούσε πρακτική στην ανάλυση, αν και ομολογουμένως δεν υπάρχουν κανόνες ανάλυσης που να διατυπώνονται ρητά.

Ωστόσο, ήταν η ανάπτυξη της «αναλυτικής» γεωμετρίας από τον ίδιο τον Ντεκάρτ –σε αντίθεση με αυτό που, αντίστοιχα, έγινε τότε γνωστό ως «συνθετική» γεωμετρία του Ευκλείδη– που τον έκανε να συνειδητοποιήσει τη σημασία της ανάλυσης και που άνοιξε μια εντελώς νέα διάσταση στην αναλυτική μεθοδολογία. Είναι σημαντικό ότι η Γεωμετρία του Ντεκάρτ δημοσιεύτηκε για πρώτη φορά μαζί με τον Λόγο και διαφημίστηκε ως δοκίμιο με τη μέθοδο που περιγράφεται στον Λόγο. Η Γεωμετρία ξεκινά με τόλμη: «Οποιοδήποτε πρόβλημα στη γεωμετρία μπορεί εύκολα να αναχθεί σε τέτοιους όρους που η γνώση των μηκών ορισμένων ευθειών είναι αρκετή για την κατασκευή του». (Ζ, 2) Ο Ντεκάρτ συνεχίζει να δείχνει πώς οι αριθμητικές πράξεις της πρόσθεσης, της αφαίρεσης, του πολλαπλασιασμού, της διαίρεσης και της εξαγωγής ριζών μπορούν να αναπαρασταθούν γεωμετρικά. Για παράδειγμα, ο πολλαπλασιασμός δύο γραμμών BD και BC μπορεί να πραγματοποιηθεί ενώνοντάς τες όπως στο παρακάτω διάγραμμα με AC, με το AB να λαμβάνεται ως μήκος μονάδας. Εάν το DE στη συνέχεια τραβηχτεί παράλληλα με το AC, το BE είναι το απαιτούμενο αποτέλεσμα. (Δεδομένου ότι ο λόγος του BD προς το BE είναι ο ίδιος με τον λόγο του AB προς το BC, τα δύο τρίγωνα BDE και BAC είναι παρόμοια, BD × BC = AB × BE = BE, αν AB είναι το μήκος μονάδας.)

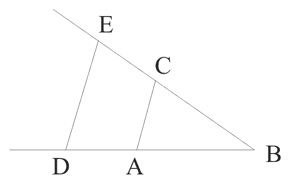
Τα προβλήματα μπορούν πράγματι στη συνέχεια να αναλυθούν σε απλούστερα προβλήματα που περιλαμβάνουν την κατασκευή μεμονωμένων ευθειών γραμμών, ενθαρρύνοντας την αποσυνθετική σύλληψη της ανάλυσης. Αλλά αυτό που έχει τη μεγαλύτερη σημασία στη Γεωμετρία του Ντεκάρτ είναι η χρήση της άλγεβρας. Αν και η εφεύρεση της άλγεβρας μπορεί επίσης να εντοπιστεί στους αρχαίους Έλληνες, κυρίως στον Διόφαντο, ο οποίος είχε εισαγάγει αριθμητικές μεταβλητές («x», «x²» κ.λπ.), μόλις τον δέκατο έκτο αιώνα η άλγεβρα τελικά καθιερώθηκε. Ο Vieta, σε ένα έργο του 1591, πρόσθεσε σχηματικά γράμματα σε αριθμητικές μεταβλητές, έτσι ώστε οι τετραγωνικές εξισώσεις, για παράδειγμα, να μπορούν στη συνέχεια να αναπαρασταθούν (με τη μορφή «ax² + bx + c = 0»), αποδίδοντας αποτελέσματα μεγαλύτερης γενικότητας. Η άλγεβρα ονομάστηκε συγκεκριμένα «τέχνη της ανάλυσης» και ήταν στο έργο του Ντεκάρτ (καθώς και του Φερμά) που πραγματοποιήθηκαν οι τεράστιες δυνατότητές της. Αποδείχθηκε πράγματι ένα ισχυρό εργαλείο ανάλυσης, επιτρέποντας την αλγεβρική αναπαράσταση πολύπλοκων γεωμετρικών σχημάτων, επιτρέποντας στους πόρους της άλγεβρας και της αριθμητικής να χρησιμοποιηθούν για την επίλυση των μετασχηματισμένων γεωμετρικών προβλημάτων.

Η φιλοσοφική σημασία δεν ήταν λιγότερο βαρυσήμαντη. Γιατί με την αναγωγή των γεωμετρικών προβλημάτων σε αριθμητικά και αλγεβρικά προβλήματα, αφαιρέθηκε η ανάγκη να επικαλεστούμε τη γεωμετρική «διαίσθηση». Πράγματι, όπως ο ίδιος ο Ντεκάρτ καθιστά σαφές στον «Κανόνα Δεκαέξι», η αναπαράσταση των πάντων αλγεβρικά –αφαιρώντας από συγκεκριμένα αριθμητικά μεγέθη καθώς και από γεωμετρικά σχήματα– μας επιτρέπει να εκτιμήσουμε ακριβώς αυτό που είναι ουσιαστικό (PW, I, 66–9.) Ο στόχος δεν είναι απλώς να λύσετε ένα πρόβλημα ή να βρείτε τη σωστή απάντηση, αλλά να αποκτήσετε μια εικόνα για το πώς λύνεται το πρόβλημα ή γιατί είναι η σωστή απάντηση. Αυτό που αποκαλύπτει η αλγεβρική αναπαράσταση είναι η δομή της λύσης στην κατάλληλη γενικότητά της. (Πρβλ. Gaukroger 1989, κεφ. 3.) Φυσικά, η «διαίσθηση» εξακολουθεί να απαιτείται, σύμφωνα με τον Ντεκάρτ, για να επιτευχθούν οι «σαφείς και διακριτές» ιδέες των θεμελιωδών αληθειών και σχέσεων που βρίσκονται στη βάση αυτού που κάνουμε, αλλά αυτό δεν θεωρήθηκε ως κάτι στο οποίο θα μπορούσαμε απλώς να απευθυνθούμε χωρίς αυστηρή εκπαίδευση σε ολόκληρη την καρτεσιανή μέθοδο.

Η περαιτέρω εφαρμογή των αλγεβρικών τεχνικών, στο πλαίσιο της ανάπτυξης της θεωρίας συναρτήσεων, επρόκειτο να οδηγήσει στη δημιουργία από τον Λάιμπνιτς και τον Νεύτωνα του διαφορικού και ολοκληρωτικού λογισμού - ο οποίος, στα μαθηματικά, ονομάστηκε «ανάλυση». Με τη σειρά του, ήταν το έργο της αυστηροποίησης του λογισμού τον δέκατο ένατο αιώνα που έπαιξε βασικό ρόλο στο έργο των Φρέγκε και Ράσελ, στο οποίο η θεωρία συναρτήσεων επεκτάθηκε στην ίδια τη λογική και εμφανίστηκε η ευρωπαϊκή αναλυτική φιλοσοφία.

3. Βρετανικός Εμπειρισμός

Η αποσυνθετική αντίληψη της ανάλυσης, όπως εφαρμόζεται σε ιδέες ή έννοιες, ήταν ιδιαίτερα χαρακτηριστική του βρετανικού εμπειρισμού. Όπως το έθεσε ο Λοκ, «όλες οι πολύπλοκες Ιδέες μας είναι τελικά επιλύσιμες σε απλές Ιδέες, από τις οποίες είναι σύνθετες και αρχικά αποτελούνται, αν και ίσως τα άμεσα Συστατικά τους, όπως μπορώ να πω έτσι, είναι επίσης σύνθετες Ιδέες» (Δοκίμιο, II, xxii, 9). Ο στόχος ήταν στη συνέχεια να δώσουμε μια περιγραφή αυτών των ιδεών, εξηγώντας πώς προκύπτουν, δείχνοντας ποιες απλούστερες ιδέες συνθέτουν τις σύνθετες ιδέες μας (π.χ. ουσίας) και διακρίνοντας τις διάφορες νοητικές λειτουργίες που εκτελούνται σε αυτές για τη δημιουργία της γνώσης και των πεποιθήσεων που έχουμε. Ο Locke χρησιμοποιεί τον όρο «Ανάλυση», ωστόσο, μόνο μία φορά σε ολόκληρο το Δοκίμιο (λίγο μετά την παρατήρηση που μόλις παρατέθηκε). Ίσως είχε επίγνωση της σημασίας της στην αρχαία ελληνική γεωμετρία, γεγονός που τον έκανε να διστάζει να τη χρησιμοποιήσει ευρύτερα, αλλά εξακολουθεί να είναι σημαντικό ότι όταν το κάνει, το κάνει ακριβώς με την έννοια της «αποσύνθεσης». Ο Λοκ τείνει να μιλάει, ωστόσο, για «συνδυασμό» ή «σύνθεση» αντί για «σύνθεση» σύνθετων ιδεών από απλούστερες ιδέες και για «διαχωρισμό» ή «επίλυση» αντί για «ανάλυση» τους σε απλούστερες ιδέες. Αλλά στην περίοδο που ακολούθησε τον Λοκ, η «ανάλυση» άρχισε να χρησιμοποιείται όλο και περισσότερο για τη διαδικασία της «ανάλυσης» των συμπλεγμάτων στα συστατικά τους.

4. Λάιμπνιτς

Ο Λάιμπνιτς καταλαμβάνει ένα κομβικό σημείο στην ιστορία των αντιλήψεων της ανάλυσης. Γνώστης τόσο της κλασικής όσο και της σύγχρονης σκέψης, στην πρώτη γραμμή τόσο των μαθηματικών όσο και της φιλοσοφίας, παρείχε μια μεγάλη σύνθεση των υπαρχουσών αντιλήψεων της ανάλυσης και ταυτόχρονα άνοιξε το δρόμο για την κυριαρχία της αποσυνθετικής αντίληψης στην ευρωπαϊκή φιλοσοφία. Το κλειδί για όλα αυτά είναι αυτό που μπορεί να ονομαστεί η αρχή του περιορισμού. Σε μια επιστολή προς τον Arnauld, γράφει: «σε κάθε καταφατική αληθινή πρόταση, αναγκαία ή ενδεχομενική, καθολική ή μοναδική, η έννοια του κατηγορήματος περιέχεται κατά κάποιο τρόπο σε εκείνη του υποκειμένου, praedicatum inest subjecto. Αλλιώς δεν ξέρω ποια είναι η αλήθεια». (PW, 62; πρβλ. PT, 87–8) Εάν αυτή η συγκράτηση του κατηγορήματος στο υποκείμενο μπορούσε τότε να γίνει σαφής, σύμφωνα με τον Leibniz, θα μπορούσε έτσι να επιτευχθεί μια απόδειξη της πρότασης. Έτσι, η απόδειξη προχωρά με την ανάλυση του υποκειμένου, με στόχο να αναχθεί η πρόταση σε αυτό που ο Λάιμπνιτς αποκαλεί «ταυτότητα» – με διαδοχικές εφαρμογές του κανόνα της «αντικατάστασης ισοδυνάμων», χρησιμοποιώντας έναν κατάλληλο ορισμό. Μια πρόταση εκφράζει μια ταυτότητα, σύμφωνα με την ορολογία του Λάιμπνιτς, εάν το κατηγόρημα είναι ρητά είτε ταυτόσημο είτε περιλαμβάνεται στο υποκείμενο (βλ. PT, 87–8). Η ακόλουθη απόδειξη του «4 = 2 + 2» απεικονίζει τη διαδικασία (πρβλ. Leibniz NE, IV, vii, 10):

α) 4 = 2 + 2
β) 3 + 1 = 2 + 2 (με τον ορισμό «4 = 3 + 1»)
γ) (2 + 1) + 1 = 2 + 2 (εξ ορισμού «3 = 2 + 1»)
δ) 2 + (1 + 1) = 2 + 2 (με συσχέτιση)
ε) 2 + 2 = 2 + 2 (με τον ορισμό «2 = 1 + 1»)

Η τελευταία γραμμή της απόδειξης είναι μια «ταυτότητα» με την έννοια του Λάιμπνιτς, και το σημαντικό σημείο σχετικά με μια ταυτότητα είναι ότι είναι «αυτονόητη» ή «γνωστή μέσω του εαυτού της», δηλαδή, μπορεί απλώς να «φανεί» ότι είναι αληθινή (πρβλ. Leibniz PW, 15; LP, 62). Θα ήταν δελεαστικό να μιλήσουμε εδώ για ταυτότητες που «διαισθητικές» ως αληθινές, αλλά ο Λάιμπνιτς τείνει να χρησιμοποιεί τη λέξη «διαίσθηση» για την άμεση κατανόηση του περιεχομένου μιας έννοιας (βλ. MKTI, 23-7), ενώ το σημείο σχετικά με τη γνώση της αλήθειας των ταυτοτήτων είναι ότι μπορούμε να το κάνουμε χωρίς να κατανοήσουμε το περιεχόμενο οποιουδήποτε από τους όρους. Στο βαθμό που μπορούμε ακόμα να κρίνουμε ότι μια τέτοια πρόταση είναι αληθινή, η γνώση μας είναι αυτό που ο Λάιμπνιτς αποκαλεί «τυφλή» ή «συμβολική» παρά «διαισθητική» (ibid., 25).

Πράγματι, ακριβώς επειδή οι αποδείξεις μπορούσαν να πραγματοποιηθούν χωρίς προσφυγή στη διαίσθηση, ο Λάιμπνιτς έλκονταν τόσο πολύ από τη συμβολική μέθοδο. Όπως παρατήρησε στα Νέα Δοκίμια, η μεγάλη αξία της άλγεβρας, ή της γενικευμένης άλγεβρας που ονόμασε «τέχνη των συμβόλων», έγκειται στον τρόπο με τον οποίο «ξεφορτώνει τη φαντασία» (NE, 488). Αν οι αποδείξεις μπορούσαν να παραχθούν καθαρά μηχανικά, τότε απελευθερώνονταν από τις ιδιοτροπίες των δικών μας νοητικών διεργασιών (βλ. NE, 75, 412). Για τον Λάιμπνιτς, η κατάσταση μιας πρότασης –η αλήθεια ή το ψεύδος, η αναγκαιότητα ή το ενδεχόμενο– εξαρτιόταν όχι από τον τρόπο αντίληψής της (όπως ήταν για τον Ντεκάρτ και τον Λοκ), ο οποίος μπορούσε να διαφέρει από άτομο σε άτομο, αλλά από τη μέθοδο απόδειξής της, η οποία ήταν ένα αντικειμενικά προσδιορίσιμο θέμα.

Η αντίληψη του Λάιμπνιτς για την ανάλυση μπορεί επομένως να θεωρηθεί ότι συνδυάζει πτυχές της μεθόδου διαίρεσης του Πλάτωνα, στην κεντρική θέση που αποδίδεται στον ορισμό των εννοιών, της αρχαίας ελληνικής γεωμετρίας και της αριστοτελικής λογικής, στην έμφαση που δίνεται στην απόδειξη και την επιστροφή στις πρώτες αρχές, και της καρτεσιανής γεωμετρίας και της νέας άλγεβρας, στην αξία που αποδίδεται στις συμβολικές διατυπώσεις. Επιπλέον, μπορούμε να δούμε πώς, κατά την άποψη του Λάιμπνιτς, η ανάλυση και η σύνθεση είναι αυστηρά συμπληρωματικές (βλ. ΗΠΑ, 16–17). Γιατί αφού μας ενδιαφέρουν μόνο οι ταυτότητες, όλα τα βήματα είναι αναστρέψιμα. Εφόσον παρέχεται η σωστή σημειογραφία και οι κατάλληλοι ορισμοί και αρχές, μπορεί κανείς να κινηθεί με την ίδια ευκολία είτε προς μια «αναλυτική» είτε προς μια «συνθετική» κατεύθυνση, δηλαδή, στο παραπάνω παράδειγμα, είτε από το (α) στο (ε) είτε από το (ε) στο (α). Εάν μπορούσε έτσι να δημιουργηθεί μια καθολική ή ιδανική λογική γλώσσα, θα είχαμε ένα σύστημα που θα μπορούσε να λειτουργήσει όχι μόνο ως διεθνής γλώσσα και επιστημονική σημειογραφία, αλλά και ως λογικός λογισμός που θα παρείχε τόσο μια λογική απόδειξης όσο και μια λογική ανακάλυψης. Το όραμα του Λάιμπνιτς μπορεί να ήταν παράλογα φιλόδοξο, αλλά το ιδανικό ήταν να επηρεάσει πολλούς μεταγενέστερους φιλοσόφους, κυρίως τον Φρέγκε και τον Ράσελ.

5. Καντ

Η αποσυνθετική αντίληψη της ανάλυσης, όπως εφαρμόζεται στις έννοιες, έφτασε στο αποκορύφωμά της στο έργο του Καντ, αν και συνέχισε να έχει επιρροή από τότε, κυρίως στις πρώιμες φιλοσοφίες του Ράσελ και του Μουρ. Όπως δείχνουν τα προ-κριτικά γραπτά του, ο Καντ απλώς υιοθετεί την αποσυνθετική αντίληψη της ανάλυσης του Λάιμπνιτς, και παρόλο που, στην κριτική του περίοδο, απορρίπτει την άποψη του Λάιμπνιτς ότι όλες οι αλήθειες είναι, με την έννοια του Λάιμπνιτς, «αναλυτικές», διατηρεί την υποκείμενη αποσυνθετική αντίληψη της ανάλυσης. Απλώς αναγνωρίζει μια περαιτέρω κατηγορία «συνθετικών» αληθειών, και μέσα σε αυτήν, μια υποκατηγορία «συνθετικών a priori» αληθειών, τις οποίες είναι το κύριο καθήκον της Κριτικής του Καθαρού Λόγου να αποσαφηνίσει.

Όπως δείχνει η «Εισαγωγή» της Κριτικής (Α6-7/Β10-11), η αποσυνθετική σύλληψη της ανάλυσης βρίσκεται στη βάση της διάκρισης του Καντ μεταξύ αναλυτικών και συνθετικών κρίσεων. Μπορούμε να διατυπώσουμε το «επίσημο» κριτήριο του Καντ για την αναλυτικότητα ως εξής:

(ΕΝΑο) Μια αληθής κρίση του τύπου «Ο Α είναι Β» είναι αναλυτική εάν και μόνον εάν το κατηγόρημα Β περιέχεται στο υποκείμενο Α.

Το πρόβλημα με αυτό το κριτήριο, όμως, ή τουλάχιστον, με τον τρόπο που το καλύπτει ο Καντ, είναι προφανές. Γιατί ποιος είναι ο κριτής του αν ένα κατηγόρημα είναι ή όχι «περιέχεται» —όσο «συγκαλυμμένα»— στο υποκείμενο; Σύμφωνα με τον Λάιμπνιτς, για παράδειγμα, όλες οι αλήθειες, ακόμη και οι ενδεχόμενες, είναι «αναλυτικές»: απλώς, στην περίπτωση μιας ενδεχόμενης αλήθειας, μόνο ο Θεός μπορεί να γνωρίζει τι «περιέχεται κρυφά» στο θέμα, δηλαδή να γνωρίζει την ανάλυσή του. Ωστόσο, η συζήτηση του Καντ για τη σύνδεση μεταξύ υποκειμένου και κατηγορήματος στις αναλυτικές κρίσεις που «εξετάζονται μέσω της ταυτότητας», προτείνει ένα πιο αντικειμενικό κριτήριο – ένα λογικό και όχι φαινομενολογικό. Αυτό γίνεται πιο σαφές αργότερα στην Κριτική, όταν ο Καντ προσδιορίζει την αρχή της αντίφασης ως «την υψηλότερη αρχή όλων των αναλυτικών κρίσεων» (A150–1/B189–91). Το εναλλακτικό κριτήριο μπορεί να διατυπωθεί ως εξής:

(ΕΝΑL) Μια αληθής κρίση της μορφής «Το Α είναι Β» είναι αναλυτική εάν και μόνον εάν η άρνησή της «Το Α δεν είναι Β» είναι αντιφατική.

Ωστόσο, σε οτιδήποτε άλλο εκτός από ασήμαντες περιπτώσεις (όπως οι «ταυτότητες» του Λάιμπνιτς), θα εξακολουθεί να απαιτείται «ανάλυση» για να αποδειχθεί ότι το «Α δεν είναι Β» είναι αυτοαντιφατικό, και για κάθε δεδομένο βήμα «ανάλυσης», φαίνεται ότι θα πρέπει ακόμα να βασιστούμε σε αυτό που είναι «σκέψη» στη σχετική έννοια. Επομένως, δεν είναι σαφές ότι (ANL) είναι μια βελτίωση στο σύστημα του Καντ.

Όποιο κριτήριο και αν προσφέρουμε για να συλλάβουμε την έννοια του Καντ για την αναλυτικότητα των κρίσεων, το θεμελιώδες σημείο αντίθεσης μεταξύ «αναλυτικών» και «συνθετικών» κρίσεων, που έχει τις ρίζες του στην αποσυνθετική αντίληψη της ανάλυσης, έγκειται στο ότι η πρώτη απλώς «αποσαφηνίζει» και η δεύτερη «επεκτείνει» τις γνώσεις μας. Αυτός ήταν ο λόγος που ο Καντ θεώρησε τις μαθηματικές προτάσεις ως συνθετικές, αφού ήταν πεπεισμένος —δικαίως— ότι τα μαθηματικά προάγουν τη γνώση μας. Αυτό γίνεται σαφές στο κεφάλαιο 1 του «Υπερβατικού Δόγματος της Μεθόδου» (CPR, A716–7/B744–5), όπου ο Καντ υποστηρίζει ότι καμία «ανάλυση» της έννοιας του τριγώνου δεν θα επιτρέψει σε έναν φιλόσοφο να δείξει ότι το άθροισμα των γωνιών ενός τριγώνου ισούται με δύο ορθές γωνίες. Χρειάζεται ένας γεωμέτρης για να το αποδείξει αυτό, κατασκευάζοντας πραγματικά το τρίγωνο και σχεδιάζοντας κατάλληλες βοηθητικές γραμμές (όπως κάνει ο Ευκλείδης στο Ι, 32 των Στοιχείων). Ο Καντ γράφει ότι «Το να κατασκευάζεις μια έννοια σημαίνει να εκθέτεις εκ των προτέρων τη διαίσθηση που αντιστοιχεί σε αυτήν» (A713/B741). Και μια τέτοια «διαίσθηση» χρειάζεται επίσης για την κατασκευή των βοηθητικών γραμμών. Σύμφωνα με τον Καντ, λοιπόν, η όλη διαδικασία είναι μια διαδικασία σύνθεσης. Η «ανάλυση», όσον αφορά τις έννοιες, έχει να παίξει τόσο μικρό ρόλο που δεν προκαλεί έκπληξη το γεγονός ότι καταδικάζεται ως άχρηστη.

Μπορεί να φαίνεται ότι ο Καντ απλώς αντέστρεψε την αρχική αντίληψη της ανάλυσης στην αρχαία ελληνική γεωμετρία —ή τουλάχιστον κατέρρευσε μαζί σε «σύνθεση» αυτό που είχε προηγουμένως διακριθεί— καθώς οι δύο δραστηριότητες που αναφέρθηκαν παραπάνω είναι και οι δύο μέρος αυτού που οι αρχαίοι γεωμέτρες ονόμαζαν ανάλυση. Ωστόσο, η ιστορία περιπλέκεται κάπως από τη διάκριση του ίδιου του Καντ μεταξύ δύο εννοιών ανάλυσης. Στην προ-κριτική εναρκτήρια διατριβή του, ο Καντ κάνει μια διάκριση μεταξύ της ανάλυσης που νοείται ως «μια παλινδρόμηση από αυτό που είναι γειωμένο στο έδαφος» και της ανάλυσης που νοείται ως «μια παλινδρόμηση από ένα σύνολο στα πιθανά ή ενδιάμεσα μέρη του... μια υποδιαίρεση μιας δεδομένης ένωσης» (TP 2: 388 n.). Η διάκριση εδώ είναι σαφώς μεταξύ οπισθοδρομικής ανάλυσης και αποσυνθετικής ανάλυσης, και είναι μια διάκριση που διατηρεί ο Καντ στα κριτικά του έργα. Έτσι, περιγράφει τη μέθοδο των Προλεγομένων του σε οποιαδήποτε μελλοντική μεταφυσική ως αναλυτική ή «οπισθοδρομική», που σημαίνει «ότι κάποιος προχωρά από αυτό που αναζητείται σαν να ήταν δεδομένο και ανεβαίνει στις συνθήκες κάτω από τις οποίες μόνο είναι δυνατό» (PFM 4: 276 n.). Παραδειγματίζοντας αυτή τη μέθοδο, ο Καντ υποθέτει τις συνθετικές γνώσεις των καθαρών μαθηματικών, ιδιαίτερα της γεωμετρίας, ως αληθινές και επιστρέφει σε αυτό που θεωρεί ότι είναι οι a priori αρχές των ανθρώπινων γνωστικών ικανοτήτων που καθιστούν δυνατές αυτές τις γνώσεις. Από αυτές τις αρχές, είναι στη συνέχεια, σύμφωνα με τον Καντ, δυνατό να εργαστεί κανείς, χρησιμοποιώντας τη συνθετική ή προοδευτική μέθοδο (όπως παραδειγματίζεται στην ΚΑΡΠΑ), μέχρι τη γνώση, π.χ. καθαρή μαθηματική γνώση. Με την αντίληψή του για την αναλυτική μέθοδο, βλέπουμε τον Καντ να εμμένει και να δίνει μια κλασική δήλωση αυτού που ο Πάππος είχε ονομάσει θεωρητική ανάλυση.

6. Ινδική Αναλυτική Φιλοσοφία

Μια ισχυρή υπόθεση μπορεί να γίνει ότι η «αναλυτική» φιλοσοφία, με μια έννοια που θα αναγνωριζόταν σήμερα, αναπτύχθηκε στην Ινδία αρκετούς αιώνες πριν από την Ευρώπη. Η υπόθεση για αυτό χτίστηκε από το πρωτοποριακό έργο του Bimal Krishna Matilal (1986, 1990, 1998a, 2001, 2005), σε έργο που χρονολογείται από τη δεκαετία του 1960, και δηλώθηκε ρητά και δυναμικά από τον Jonardon Ganeri. Η εστίαση εδώ είναι στις μορφές ανάλυσης που εμπλέκονται που δικαιολογούν τον χαρακτηρισμό αυτής της ινδικής παράδοσης «αναλυτικής» με τη σύγχρονη έννοια.

Το ιδρυτικό κείμενο της (πρώιμης σύγχρονης) ινδικής αναλυτικής φιλοσοφίας ήταν το Κόσμημα του Στοχασμού για την Αλήθεια (Tattvacintāmaṇi) του Gaṅgeśa, που χρονολογείται από τις αρχές του δέκατου τέταρτου αιώνα, το οποίο υπερασπίστηκε τις ιδέες της πρώιμης σχολής Nyāya από τις σκεπτικιστικές επιθέσεις των βουδιστών επιστημολόγων, και ως εκ τούτου έγινε γνωστό ως Navya-Nyāya ή νέα σχολή Nyāya. Οι ιδέες επεξεργάστηκαν από διαδοχικούς στοχαστές τους επόμενους τέσσερις αιώνες, κυρίως από τους Raghunātha, Jagadīśa και Gadādhara. Μια έκθεση των απόψεων του Gadādhara δόθηκε στο The Manual of Reason (Tarkasaṃgraha) του Annambhaṭṭa, στο οποίο ο Ganeri βασίζει κυρίως την αφήγησή του στην Αναλυτική Φιλοσοφία στην Πρώιμη Σύγχρονη Ινδία. Τα έντεκα θέματα που συζητά ο Ganeri θα αναγνωρίζονταν όλα από οποιονδήποτε αναλυτικό φιλόσοφο σήμερα ως κεντρικά για τις δικές του ανησυχίες: η θεωρία των κατηγοριών και του ορισμού. φυσική ουσία· χώρος, χρόνος και κίνηση. εαυτούς? φιλοσοφική ψυχολογία; αιτιώδης συνάφεια· αντίληψη; λογικό συμπέρασμα; νόημα και κατανόηση· καθολικά? οντολογία. Οι έννοιες ορίζονται ρητά, δοκιμάζονται και βελτιώνονται. Οι θέσεις διατυπώνονται προσεκτικά, με όλο και πιο τεχνική γλώσσα, και οι αντιρρήσεις διατυπώνονται και απαντώνται, ανάλογα με την περίπτωση. και υπάρχει μια ισχυρή αίσθηση ότι στοχεύουμε στην «αλήθεια», όπως αντικατοπτρίζεται στον ίδιο τον τίτλο του ιδρυτικού κειμένου του Gaṅgeśa.

Ο στόχος του Gaṅgeśa ήταν να υπερασπιστεί τον θεμελιώδη ισχυρισμό της σχολής Nyāya ότι το «ύψιστο καλό» επιτυγχάνεται όταν κατανοούμε τη φύση του καλού συλλογισμού και τις πηγές της γνώσης, όπως αναφέρεται περίφημα στην εισαγωγή της Nyāya-sūtra. Ένας φυσικός τρόπος για να προχωρήσουμε θα ήταν να εντοπίσουμε τα πράγματα που γνωρίζουμε και στη συνέχεια να διερευνήσουμε πώς τα γνωρίσαμε. Αλλά αυτό προϋποθέτει ότι μπορούμε να προσδιορίσουμε τα πράγματα που γνωρίζουμε, και αυτό ακριβώς είναι το επίμαχο, καθώς οι (βουδιστές) σκεπτικιστές είχαν πιέσει εναντίον της σχολής Nyāya. Και αν υποχωρήσουμε σε μια πιο μετριοπαθή θέση, ότι χρειάζεται απλώς να προσδιορίσουμε τις αληθινές πεποιθήσεις, τότε εξακολουθεί να τίθεται το σκεπτικιστικό ερώτημα για το πώς μπορούμε να διακρίνουμε μεταξύ αληθινών και ψευδών πεποιθήσεων. Μια σειρά από απόψεις αναπτύχθηκαν ως απάντηση σε αυτά τα θεμελιώδη ερωτήματα, απόψεις που έγιναν όλο και πιο περίπλοκες καθώς προχωρούσε η συζήτηση (για συζήτηση, βλ. Ganeri 2011, Μέρος III). Η σύγκριση μεταξύ αυτής της συζήτησης και της συνεχιζόμενης συζήτησης σχετικά με τον ορισμό της γνώσης στη σύγχρονη (δυτική) αναλυτική φιλοσοφία είναι εντυπωσιακή. Η ανάλυση ως επιδίωξη ορισμού μιας έννοιας με τη διατύπωση αναγκαίων και επαρκών συνθηκών, τη δοκιμή οποιουδήποτε υποψήφιου ορισμού με παραδείγματα και αντιπαραδείγματα και την ανάλογη αναθεώρηση, είναι τόσο βασική για την ινδική επιστημολογία όσο και για την αναλυτική επιστημολογία σήμερα.

Ας επιστρέψουμε στη βασική συμπερασματική μορφή της ινδικής λογικής –στην τριμελή εκδοχή της– για να δώσουμε ένα δεύτερο παράδειγμα για το πώς η σχολή Navya-Nyāya ανέπτυξε την αναλυτική της μεθοδολογία:

(1) Θέση (pakṣa): Αυτό το βουνό κατέχει φωτιά. (p έχει s)

(2) Λόγος (hetu): Αυτό το βουνό έχει καπνό. (Το p έχει h)

(3) Διείσδυση (vyāpti): Ό,τι κατέχει καπνό είναι πυρκαγιό. (Ό,τι έχει h έχει s)

Όπως σημειώθηκε στη συμπληρωματική ενότητα για τη Μεσαιωνική Ινδική Φιλοσοφία, υπάρχουν δύο σχέσεις εδώ, η σχέση της κατοχής και η σχέση της διείσδυσης. Η πρώτη είναι η πιο θεμελιώδης σχέση, και η ινδική λογική έχει πράγματι περιγραφεί ως λογική κατοχής ιδιοκτησίας (Bhattacharyya 1987, Matilal 1998). Αλλά η «ιδιοκτησία» εδώ πρέπει να γίνει κατανοητή με μια ευρύτερη έννοια από ό,τι συνηθίζεται στα αγγλικά. Διότι το να πούμε ότι το p έχει s (το sādhya), κατά την ινδική άποψη, σημαίνει ότι το p είναι ο τόπος στον οποίο εμφανίζεται το s, έτσι ώστε η αντίστροφη σχέση εδώ είναι η εμφάνιση. Το να πούμε ότι ένα δοχείο είναι στο τραπέζι, για παράδειγμα, σημαίνει ότι το τραπέζι είναι ο τόπος στον οποίο εμφανίζεται ένα δοχείο, δηλαδή ότι το τραπέζι έχει δοχείο. Εδώ λοιπόν το δοχείο γίνεται κατανοητό ως «ιδιότητα» του τραπεζιού. Αυτό αποτυπώνεται —ή υπογράφεται— από έναν κανόνα γραμματικής που διατύπωσαν οι λογικοί Navya-Nyāya, ακολουθώντας τη γραμματική του Pāṇini. Σύμφωνα με αυτόν τον κανόνα, κάποιος καθορίζει τη sādhya ενός συμπεράσματος, όπου η «θέση» είναι της μορφής «p είναι s-possessing», αφαιρώντας το επίθημα «-possessing», έτσι ώστε οι «ιδιότητες» στα δύο παραδείγματα που μόλις δόθηκαν να είναι «φωτιά» και «pot», αντίστοιχα. Αναπτύχθηκαν περίπλοκες θεωρίες για τον εντοπισμό και την αποσαφήνιση όλων των διαφόρων «ιδιοτήτων», που έχουν τις ρίζες τους στους σχετικούς κανόνες της σανσκριτικής γραμματικής. Και πάλι, για να δώσω μόνο ένα παράδειγμα, εάν ένα τραπέζι έχει γλάστρα, τότε αυτό το τραπέζι μπορεί να αναφέρεται με το όνομα «αυτό το [πράγμα] που έχει γλάστρα». Το πάτωμα στο οποίο βρίσκεται το τραπέζι μπορεί στη συνέχεια να περιγραφεί ως «[αυτό] (που κατέχει)-κατέχει» και ούτω καθεξής. (Για συζήτηση, βλ. Bhattacharyya 1987.)

Όσον αφορά τη σχέση διείσδυσης, είναι σημαντικό να εκτιμήσουμε ότι αυτή είναι πιο περίπλοκη από μια απλή σχέση μεταξύ h και s: είναι μια σχέση μεταξύ h όπως συμβαίνει στο p και s όπως συμβαίνει στο p. Η σχέση εμφάνισης δεν χρειάζεται να είναι η ίδια στις δύο περιπτώσεις, κατά την άποψη Navya-Nyāya, ανοίγοντας περίπλοκες έρευνες ως προς το ποιες ακριβώς μπορεί να είναι οι σχέσεις που εξακολουθούν να επιτρέπουν τη θεμελίωση του συμπεράσματος. (Και πάλι, για συζήτηση, βλ. Bhattacharyya 1987.) Σε αυτό το σημείο είναι επίσης σημαντικό να επιστρέψουμε στην αρχική πρώιμη εκδοχή του συμπεράσματος Nyāya, στην οποία το τρίτο μέλος συμπεριέλαβε παραδείγματα στην «επιβεβαίωση»:

(3) Επιβεβαίωση (drṣṭānta): Ό,τι έχει καπνό έχει φωτιά, όπως η κουζίνα, σε αντίθεση με τη λίμνη.

Αυτό που προσφέρεται εδώ είναι ένα θετικό (sapakṣa) και ένα αρνητικό (vipakṣa) παράδειγμα. Αν δούμε καπνό να βγαίνει από μια κουζίνα, τότε μπορούμε πράγματι να συμπεράνουμε ότι η φωτιά είναι η αιτία. Μια λίμνη μπορεί μερικές φορές να φαίνεται σαν να έχει καπνό, παρά το γεγονός ότι δεν υπάρχει φωτιά, αλλά με μια πιο προσεκτική έρευνα, αυτό αποδεικνύεται ότι είναι ομίχλη, και ως εκ τούτου δεν αποτελεί αντιπαράδειγμα, παρέχοντας «αρνητικά» επιβεβαίωση. Σύμφωνα με την άποψη Navya-Nyāya, είναι τα (εμπειρικά) παραδείγματα που παρέχουν τα στοιχεία για τη σχετική σχέση διείσδυσης. (Βλ. π.χ. Matilal 1998, 194–200.) Έτσι, η «ανάλυση» εδώ περιλαμβάνει επίσης την εύρεση των πιο πειστικών παραδειγμάτων - και την απόδειξη ότι τα προφανή αντιπαραδείγματα δεν είναι στην πραγματικότητα αντιπαραδείγματα.

Οι οπισθοδρομικές και αποσυνθετικές αντιλήψεις της ανάλυσης βρίσκονται σαφώς στη μεθοδολογία Navya-Nyāya, αλλά όχι λιγότερο σημαντικός είναι ο ρόλος που διαδραματίζει η ερμηνευτική ανάλυση. Οι προτάσεις που πρέπει να αναλυθούν αναδιατυπώνονται σε μια γλώσσα που γινόταν όλο και πιο τεχνική όσο προχωρούσε η συζήτηση. Αυτή η γλώσσα ήταν η σανσκριτική, η οποία έφερε μαζί της τα δικά της χαρακτηριστικά γνωρίσματα, το πιο θεμελιώδες από τα οποία θα μπορούσε να περιγραφεί ως η δομή locus-locatee και όχι η δομή υποκειμένου-κατηγορήματος που θεωρείται βασική από πολλούς Ευρωπαίους λογικούς από τον Αριστοτέλη και μετά. Αυτό αντικατοπτρίστηκε σε μια διαφορετική αντίληψη της «πρότασης». Αυτό που εκφράζει μια πρόταση στα σανσκριτικά, σύμφωνα με την άποψη Navya-Nyāya, είναι μια ποιοτική γνωστική κατάσταση (viśiṣṭa-jñāna), «μια κατάσταση όπου ο γνώστης γνωρίζει κάτι (ή κάποιο μέρος ή κάποιο τόπο...) ως χαρακτηρισμένο από μια ιδιότητα ή έναν προσδιορισμό», όπως το περιγράφει ο Matilal (1998, 201). Αυτό που είναι προσδιορισμένο μπορεί να ονομαστεί qualificand, οπότε θα μπορούσαμε επίσης να περιγράψουμε τη θεμελιώδη δομή εδώ ως δομή qualificand-qualifier.

Ας επιστρέψουμε στην επιστημολογική συζήτηση με την οποία αρχίσαμε να δίνουμε ένα παράδειγμα για το πώς χρησιμοποιήθηκε η ανάπτυξη μιας τεχνικής γλώσσας για την επίλυση ορισμένων από τις διαφορές. Στην αφήγηση αυτής της συζήτησης, ο Ganeri συζητά το Πολύτιμο Κόσμημα της Λογικής του Mahādeva, που γράφτηκε τη δεκαετία του 1690, το οποίο έχει ως πρότυπο το Jewel of Reflection on the Truth του Gaṅgeśa. Το κλειδί για την απάντηση του Gaṅgeśa στον σκεπτικισμό ήταν η ιδέα μιας πηγής γνώσης (pramāṇa) που συνίσταται πρώτα στην αμφιβολία, στο να είσαι αναποφάσιστος μεταξύ δύο εναλλακτικών λύσεων και στη συνέχεια να επιλύεις αυτή την αμφιβολία διαπιστώνοντας ότι τα στοιχεία ευνοούν μία από αυτές τις εναλλακτικές. Ο Mahādeva ενδιαφερόταν να κάνει αυτή την ιδέα πιο ακριβή, ξεκινώντας με τον προσδιορισμό της ίδιας της αμφιβολίας. Ας υποθέσουμε ότι η αμφιβολία μας παίρνει τη μορφή σκέψης «Είναι το βουνό φωτιά ή όχι;». Καθώς ο Ganeri παρουσιάζει την άποψη του Mahādeva, η σκέψη εδώ έχει την ακόλουθη λογική μορφή:

Μια γνώση της οποίας η εξειδίκευση είναι, όπως οριοθετείται από το βουνό, εξαρτάται από έναν χαρακτηρισμό που οριοθετείται από τη φωτιά, όντας επίσης μια γνώση της οποίας η εξειδίκευση είναι, όπως οριοθετείται από το βουνό, εξαρτάται από έναν χαρακτηρισμό που οριοθετείται από την απουσία της φωτιάς. (Αναφέρεται στο Ganeri 2011, 155)

Μπορούμε να δούμε εδώ τη χρήση της τεχνικής γλώσσας των λογικών Navya-Nyāya, η οποία περιλαμβάνει όρους όπως «οριοθετείται από» (avacchinna) και «εξαρτάται από» (nirūpita) καθώς και «qualificandumness» (viśeṣyatā) και «qualifierness» (viśeṣanatā). (Για περαιτέρω συζήτηση, βλ. Ganeri 2011, κεφ. 11· και για αξιολόγηση της τεχνικής γλώσσας, κεφ. 15.)

Ο όρος «απουσία πυρός» εδώ αξίζει επίσης σύντομο σχόλιο. Μία από τις άλλες σημαντικές συζητήσεις στην πρώιμη σύγχρονη ινδική φιλοσοφία αφορούσε τη σημασία και την αντιμετώπιση των κενών όρων, όπως ακριβώς έγινε αργότερα στην πρώιμη ευρωπαϊκή αναλυτική φιλοσοφία. Τι σημαίνει, για παράδειγμα, η «απουσία πυρός»; Μερικοί φιλόσοφοι το θεώρησαν ότι υποδηλώνει αυτό που κυριολεκτικά φαίνεται να υποδηλώνει, δηλαδή, μια «πραγματική» απουσία φωτιάς, την οποία ήταν πρόθυμοι να επιτρέψουν να γίνει αντιληπτή άμεσα. Άλλοι προσπάθησαν να «αναλύσουν» μια τέτοια προφανή αναφορά με κατάλληλη παράφραση (αντλώντας από τις πηγές της σανσκριτικής γραμματικής), όπως επρόκειτο να κάνει ο Ράσελ στη θεωρία του για τις περιγραφές. (Για περαιτέρω συζήτηση αυτής της συζήτησης, βλ. Matilal 2005, κεφ. 4.) Πολλά άλλα παραδείγματα θα μπορούσαν να δοθούν για την πλούσια μη κενότητα του όρου «ινδική αναλυτική φιλοσοφία».

7. Dai Zhen και Κινεζική Φιλολογική Ανάλυση

Η πρώιμη σύγχρονη περίοδος στην Κίνα -ή με κινεζικούς όρους, η (ύστερη) δυναστεία των Μινγκ (1368–1644) και το πρώτο μισό της δυναστείας Τσινγκ (1644–1911)– ήταν μια περίοδος κατά την οποία ο Νεοκομφουκιανισμός των Σονγκ-Μινγκ έδωσε τη θέση του σε έναν πιο φιλολογικό Κομφουκιανισμό που βασιζόταν στην κειμενική επιστήμη ή στην «αποδεικτική έρευνα» (kǎozhèng 考證). Η ηθική μεταφυσική, όπως την είχε ονομάσει ο Μου Ζονγκ-σαν, του Κομφουκιανισμού Σονγκ-Μινγκ επικρίθηκε για την υιοθέτηση μιας υπερβολικά μεταφυσικής αντίληψης του lǐ (理), διαχωρίζοντας τις ηθικές αρχές από τα φυσικά ανθρώπινα συναισθήματα και επιθυμίες και βασιζόμενη υπερβολικά στην υποκειμενική ενδοσκόπηση. Βασικοί κριτικοί ήταν ο Χουάνγκ Ζονγκσί (黃宗羲 1610–1695), ο Γκου Γιανγού (顧炎武 1613–82), ο Γουάνγκ Φούζι (王夫之 1619–92) και ο Ντάι Ζεν (戴震 1723–77). Η εστίαση εδώ είναι στον Dai, ο οποίος αποτελεί το καλύτερο παράδειγμα της φιλολογικής στροφής στον Κομφουκιανισμό στο κύριο έργο του, An Evidential Commentary on the Meanings of Terms in the Mengzi, που ολοκληρώθηκε ένα χρόνο πριν πεθάνει.

Ο Ng διακρίνει τέσσερις «κυρίαρχους τρόπους ή ιδανικούς τύπους» της φιλοσοφίας των Τσινγκ: τον βιταλισμό, τον ιστορικισμό, τον ωφελιμισμό και τον διανοουμενισμό. Το πρώτο και το τρίτο, ειδικά, χαρακτηρίζουν τη φιλοσοφία του kǎozhèng, τον ιστορικισμό στην ανησυχία του για την αποκάλυψη του νοήματος των προηγούμενων ανθρώπινων ιδεών και πράξεων σε όλη τους την εξαρτώμενη από το πλαίσιο ενδεχομενικότητα και ιδιαιτερότητά τους, και τον διανοουμενισμό στην έμφαση που δίνει στη στενή ανάγνωση των κειμένων των αρχαίων κλασικών, ενημερωμένη από αιώνες σχολίων. Αυτοί οι δύο τρόποι σίγουρα χαρακτηρίζουν τη φιλοσοφία του Dai Zhen.

Η κύρια αντίρρηση του Ντάι στον Κομφουκιανισμό Σονγκ-Μινγκ αφορά την απόκλισή τους, όπως τον βλέπει, από τον αρχικό Κομφουκιανισμό του Κονγκζί και του Μενγκζί, αποτέλεσμα της ολέθριας επιρροής των μεταγενέστερων Ταοϊστικών και Βουδιστικών ιδεών. Η κατανόηση του lǐ (理), που σημαίνει «μοτίβο» ή «αρχή», είναι κεντρική στη διαμάχη. Ο Dai ξεκινά το Αποδεικτικό Σχόλιό του εξηγώντας τη δική του αντίληψη:

Η λέξη «lǐ» [理] είναι ένα όνομα που αποδίδεται στη διάταξη των μερών οποιουδήποτε πράγματος που δίνει στο σύνολο τη διακριτική του ιδιότητα ή χαρακτηριστικό και το οποίο μπορεί να παρατηρηθεί με προσεκτική εξέταση και ανάλυση των μερών μέχρι την παραμικρή λεπτομέρεια. Γι' αυτό μιλάμε για το lǐ της διαφοροποίησης [fēnlǐ 分理]. Αναφορικά με την ουσία των πραγμάτων, υπάρχουν εκφράσεις όπως το lǐ που διέπει τις ίνες [jīlǐ 理], το lǐ που διέπει τη διάταξη μεταξύ δέρματος και σάρκας [còulǐ 腠理] και το lǐ που διέπει τις τέχνες [wénlǐ 文理]. ... Όταν γίνει η σωστή διαφοροποίηση, θα υπάρχει τάξη χωρίς σύγχυση. Αυτό ονομάζεται lǐ της διευθέτησης» [tiáolǐ 條理]. (Ένα αποδεικτικό σχόλιο σχετικά με τις έννοιες των όρων στο Mengzi, ενότητα 1, tr. στο Chin and Freeman 1990, 69, αναφέρεται στο Cheng 2009, 461, tr. τροποποιήθηκε)

Ο όρος «lǐ» εδώ έχει μείνει αμετάφραστος. Στη μετάφραση από την οποία προέρχεται αυτό το απόσπασμα, αποδίδεται ως «αρχή», κάτι που μπορεί να είναι κατάλληλο για να μιλήσουμε για το «lǐ της διαφοροποίησης», αλλά το «μοτίβο» φαίνεται πιο κατάλληλο για να μιλήσουμε ακριβώς στην αρχή για «τη διάταξη των μερών οποιουδήποτε πράγματος που δίνει στο σύνολο τη διακριτική του ιδιότητα ή χαρακτηριστικό». Πράγματι, το «μοτίβο» χρησιμοποιείται στη μετάφραση του «wénlǐ» (文理), το οποίο έχει αντικατασταθεί εδώ από το «το lǐ που διέπει τις τέχνες». Όπως το ερμηνεύει ο Dai, το «lǐ» δεν είναι κάποιο είδος μεταφυσικής «αρχής» που κρύβεται πίσω από τις υποτιθέμενες έμφυτες ηθικές μας ικανότητες, αλλά απλώς το «μοτίβο» των πραγμάτων με το οποίο προσπαθούμε να σκεφτούμε ή να ενεργήσουμε σε συμφωνία. Αυτό που κάνει έτσι ο Dai είναι να επαναφέρει το «lǐ» από τη μεταφυσική του στην καθημερινή του χρήση (βλ. Wittgenstein, PI, §116).

Αντλώντας και από τις δύο σημασίες του (στα αγγλικά), το «lǐ» θα μπορούσε να χαρακτηριστεί ως (περιγραφικά) το μοτίβο των πραγμάτων, της σκέψης ή της δράσης σύμφωνα με το οποίο πρέπει (κανονιστικά) να κάνουμε την αρχή μας. Οι δύο έννοιες του «προτύπου» και της «αρχής» είναι επομένως συμπληρωματικές (συνδέοντας το περιγραφικό και το κανονιστικό). Ο όρος «fēnlǐ» (分理) είναι σημαντικός εδώ. Θα μπορούσε να μεταφραστεί ως «η αρχή της ανάλυσης». Ο όρος «fēn» (分) σημαίνει «διαιρώ» ή «διαχωρίζω» και αποτελεί μέρος ενός από τους κινεζικούς όρους που χρησιμοποιούνται σήμερα για «ανάλυση» ή «ανάλυση»: «fēnxī» (分析), όπου «xī» (析) σημαίνει επίσης «διαιρώ» ή «διαχωρίζω». Το «fēnxī» εδώ σημαίνει ξεκάθαρα «ανάλυση» με την αποσυνθετική έννοια. Ο Dai συνεχίζει να παραθέτει από μια επιλογή αρχαίων κειμένων για να απεικονίσει αυτή την αντίληψη (και τώρα στη μετάφραση του Tiwald, όπου το «lǐ» μεταφράζεται γενικά ως «Μοτίβο»):

Το Μέσο λέει: «Με προσεκτική εξέταση των εκλεπτυσμένων Προτύπων, [ο σοφός] είναι σε θέση να διακρίνει τα πράγματα το ένα από το άλλο». Το "Record of Music" λέει: «Η μουσική με την κατάλληλη έννοια μπορεί να διαποτίσει και να συνδέσει το Πρότυπο στις ανθρώπινες σχέσεις». Όπως εξηγεί ο Zhèng Xuán στο σχόλιό του για το απόσπασμα, «το να είσαι καλά διατεταγμένος [lǐ] σημαίνει να διαχωρίζεσαι σε μέρη [fēn]». Στον πρόλογό του στην Εξήγηση των Απλών και Σύνθετων Χαρακτήρων, ο Xǔ Shèn λέει: «Γνωρίζοντας το μοτίβο για τον διαχωρισμό των πραγμάτων, τα πράγματα μπορούν να διακριθούν αμοιβαία». (Ένα αποδεικτικό σχόλιο σχετικά με τις έννοιες των όρων στο Mengzi, Ενότητα 1, tr. J. Tiwald, στο Tiwald and Van Norden 2014, 321)

Η αποσυνθετική έννοια της «ανάλυσης» είναι σαφώς κυρίαρχη εδώ. Αλλά όταν μιλάμε για «γνώση του μοτίβου», υπάρχει σιωπηρή έκκληση στη συνδετική αίσθηση. Γιατί ο στόχος της κατανόησης του lǐ ενός πράγματος είναι να εντοπίσουμε τα μέρη του στη διασύνδεσή τους. Η γνώση του μοτίβου είναι αυτό που μας δίνει τη δυνατότητα να αναγνωρίσουμε τα μέρη. Η χρήση του όρου «tiáolǐ» (條理) στο εισαγωγικό απόσπασμα είναι αποκαλυπτική. Το «tiáo» σημαίνει «διάταξη» ή «τάξη», αλλά μπορεί επίσης να σημαίνει «κλαδί» ή «κλαδί» ή μπορεί να λειτουργήσει ως λέξη-μέτρο για μακρόστενα αντικείμενα (βλ. την καταχώριση στο Kroll 2022). Έτσι, το «tiáolǐ» θα μπορούσε να μεταφραστεί ως «η αρχή της αποσύνδεσης». Η ιδέα θα ήταν μέρη από κάτι τόσο αλληλένδετο που πρέπει να τα διαχωρίσουμε για να κατανοήσουμε την πραγματική δομή της σύνθεσης. Η γνώση του μοτίβου, λοιπόν, συνίσταται στο να μπορείς να διακρίνεις τα μέρη. Τελικά, μπορούμε να γνωρίζουμε το μοτίβο ενός πράγματος μόνο όταν εκτιμούμε την αποσυνθετική-συνθετική δομή του. Δεν ξέρουμε πραγματικά πώς να διαιρέσουμε κάτι ή να αναλύσουμε κάτι, θα μπορούσαμε να πούμε, εκτός αν μπορέσουμε να το συναρμολογήσουμε ξανά.

Αυτά τα δύο αποσπάσματα από την πρώτη ενότητα του Αποδεικτικού Σχολίου του Ντάι απεικονίζουν τη φιλολογική του μέθοδο. Επιχειρηματολογώντας ενάντια στον Κομφουκιανισμό Σονγκ-Μινγκ και αναπτύσσοντας τις δικές του απόψεις, διευκρινίζει τις έννοιες των βασικών όρων ορίζοντας τους και επεξηγώντας τη χρήση τους, ειδικά τη χρήση τους στους κλασικούς του Κομφουκιανισμού. Το κοσκίνισμα των χρήσιμων και διορατικών από τις παραπλανητικές και συγκεχυμένες αφηγήσεις στα ογκώδη σχόλια ανά τους αιώνες ήταν ένα ουσιαστικό μέρος αυτού. Ο Dai γράφει ότι «μόνο όταν κατανοηθούν οι Κλασικοί μπορούν να κατανοηθούν ο λόγος και το νόημα [των πραγμάτων] όπως προορίζονται από τους σοφούς και τους άξιους». Η φιλολογία ήταν επομένως το μέσο για την άσκηση φιλοσοφίας, σύμφωνα με την αντίληψη του Dai για τη φιλοσοφία (βλ. Cheng 2009, 461). Στην προσπάθειά της να επιστρέψει στους αρχαίους κλασικούς, η φιλολογική ανάλυση παρουσιάζει επίσης την οπισθοδρομική αντίληψη της ανάλυσης: οι αρχικές έννοιες, στο σταδιακό ξεδίπλωμά τους μέσω των σχολίων (σωστά ερμηνευμένων), εξηγούν πώς πρέπει να χρησιμοποιούνται και να κατανοούνται οι όροι σήμερα.

Για περαιτέρω συζήτηση, βλέπε Cheng 2009, §4; τις σημειώσεις του μεταφραστή του Tiwald στα αποσπάσματα από το αποδεικτικό σχόλιο του Dai στο Tiwald and Van Norden 2014, §51.

8. Συμπέρασμα

Στην πρώιμη σύγχρονη περίοδο, η αποσυνθετική αντίληψη της ανάλυσης ήρθε στο προσκήνιο σε πολλές φιλοσοφικές παραδόσεις. Μπορούμε να το δούμε αυτό στο έργο του Ντεκάρτ στην αναλυτική γεωμετρία, στη βρετανική εμπειριστική θεώρηση απλών και σύνθετων ιδεών, στην αντίληψη του Λάιμπνιτς για την απόδειξη, στην ιδέα του Καντ για την αναλυτικότητα, στην ινδική γλωσσολογική και σημασιολογική ανάλυση και στην εξήγηση του Ντάι Τζεν για το lǐ. Αλλά παρουσιάζονται και άλλες αντιλήψεις. Η οπισθοδρομική αντίληψη μπορεί να βρεθεί στην Εναρκτήρια Διατριβή του Καντ και να εκδηλωθεί ρητά στη μέθοδο των Προλεγομένων του. Απεικονίζεται επίσης στην ανησυχία των λογικών Navya-Nyāya να προσδιορίσουν τους κανόνες και τις αρχές που διέπουν τις λογικές τους αναλύσεις, που έχουν τις ρίζες τους στη σανσκριτική γραμματική. Η ερμηνευτική σύλληψη ενημερώνει την ανάπτυξη της ολοένα και πιο τεχνικής γλώσσας που χρησιμοποιούσαν οι Ινδοί λογικοί για να προσφέρουν τους ορισμούς και τις αναλύσεις τους και ήταν σιωπηρή στην ίδια την ιδέα της αναλυτικής γεωμετρίας, σύμφωνα με την οποία τα παραδοσιακά γεωμετρικά προβλήματα λύνονταν μεταφράζοντάς τα στη γλώσσα της αριθμητικής και της άλγεβρας. Η ερμηνευτική σύλληψη επρόκειτο να αναπτυχθεί στους αιώνες που ακολούθησαν, ειδικά στην αναλυτική παράδοση που εμφανίστηκε γύρω στις αρχές του εικοστού αιώνα στην Ευρώπη.