 Παρόλο που οι περισσότεροι άνθρωποι συνδέουν τη μαθηματική σταθερά π με κύκλους και τόξα, οι μαθηματικοί έχουν συνηθίσει να τη βλέπουν σε διάφορους τομείς. Όμως, δύο επιστήμονες του Πανεπιστημίου του Rochester εξεπλάγησαν ακόμα περισσότερο όταν διαπίστωσαν ότι το π καιροφυλακτούσε σε έναν τύπο της κβαντικής μηχανικής για τις ενεργειακές καταστάσεις του ατόμου του υδρογόνου.
Παρόλο που οι περισσότεροι άνθρωποι συνδέουν τη μαθηματική σταθερά π με κύκλους και τόξα, οι μαθηματικοί έχουν συνηθίσει να τη βλέπουν σε διάφορους τομείς. Όμως, δύο επιστήμονες του Πανεπιστημίου του Rochester εξεπλάγησαν ακόμα περισσότερο όταν διαπίστωσαν ότι το π καιροφυλακτούσε σε έναν τύπο της κβαντικής μηχανικής για τις ενεργειακές καταστάσεις του ατόμου του υδρογόνου.«Δεν βρήκαμε απλά το π», είπε η Tamar Friedmann, επισκέπτης επίκουρος καθηγήτρια μαθηματικών και επιστημονικός συνεργάτης της Φυσικής Υψηλών Ενεργειών και μια από τους συγγραφείς της μελέτης που δημοσιεύθηκε αυτή την εβδομάδα στην Journal of Mathematical Physics, «βρήκαμε την κλασική φόρμουλα του 17ου αιώνα, του Wallis για το π, καθιστώντας μας τους πρώτους που το παράγουν γενικά από τη φυσική και την κβαντομηχανική, ειδικότερα».
Ο τύπος του Wallis, που αναπτύχθηκε από τον Βρετανό μαθηματικό John Wallis, στο βιβλίο του Arithmetica infinitorum, προσδιορίζει το π ως γινόμενο μιας άπειρης σειράς λόγων που απαρτίζεται από ακέραιους αριθμούς. Για την Friedmann, η ανακάλυψη του τύπου του Wallis για το π σε μια σχέση της κβαντομηχανικής για ενεργειακές καταστάσεις του ατόμου του υδρογόνου, υπογραμμίζει την πανταχού παρουσία του π, στα μαθηματικά και την φυσική.
«Η τιμή του π έχει πάρει μυθική διάσταση, εν μέρει, επειδή είναι αδύνατο να γραφτεί με ακρίβεια 100%», είπε η Friedmann. «Δεν μπορεί να εκφραστεί με ακρίβεια ακόμη και ως λόγος ακεραίων και, αντί αυτού, παριστάνεται καλύτερα ως τύπος».
Δεν ήταν στόχος της Friedmann να ψάξει για το π, ούτε για τον τύπο του Wallis. Η ανακάλυψη ξεκίνησε σε ένα μάθημα κβαντομηχανικής που διδάσκεται από τον Carl Hagen, καθηγητή φυσικής στο Πανεπιστήμιο του Rochester και έναν από τους έξι φυσικούς που προέβλεψαν την ύπαρξη του μποζονίου Higgs. Παρόλο που οι κβαντικοί υπολογισμοί που αναπτύχθηκαν από τον Δανό φυσικό Niels Bohr στις αρχές του εικοστού αιώνα δίνουν ακριβείς τιμές για τις ενεργειακές καταστάσεις του υδρογόνου, ο Hagen θέλησε οι σπουδαστές του να χρησιμοποιήσουν μια εναλλακτική μέθοδο, που ονομάζεται μεταβολική αρχή, για να προσεγγίσουν την τιμή για την βασική κατάσταση του ατόμου του υδρογόνου. Όπως και με τον τύπο του Wallis, η μεταβολική αρχή χρονολογείται από τον 17ο αιώνα, με μια από τις πρώτες εφαρμογές της να είναι η αρχή του ελάχιστου χρόνου του μαθηματικού Pierre de Fermat, σύγχρονου του Wallis. Ο Hagen άρχισε επίσης να σκέφτεται σχετικά με το εάν θα ήταν δυνατό να εφαρμόσει αυτή τη μέθοδο σε καταστάσεις άλλες εκτός από την βασική κατάσταση. Ο Hagen ενέπλεξε την Friedmann για να να επωφεληθεί από την ικανότητά της να εργαστεί και στη φυσική και στα μαθηματικά.
Αν και η εφαρμογή της μεταβολικής αρχής για τον υπολογισμό της βασικής κατάστασης ενός ατόμου υδρογόνου είναι ένα σχετικά απλό πρόβλημα, η εφαρμογή της σε μια διεγερμένη κατάσταση δεν είναι καθόλου προφανής. Αυτό συμβαίνει επειδή η μεταβολική αρχή δεν μπορεί συνήθως να εφαρμοστεί εάν υπάρχουν χαμηλότερα ενεργειακά επίπεδα. Ωστόσο, η Friedmann και ο Hagen μπόρεσαν να το αποφύγουν αυτό με το διαχωρισμό του προβλήματος σε μια σειρά l προβλημάτων, καθένα από τα οποία επικεντρώθηκε στο χαμηλότερο ενεργειακό επίπεδο για ένα δεδομένο τροχιακό κβαντικό αριθμό, l.
Μπόρεσαν τότε να υπολογίσουν τις τιμές για τις διαφορετικές ενεργειακές καταστάσεις και να τις συγκρίνουν με τις τιμές που υπολογίστηκαν από τον Bohr, σχεδόν πριν από έναν αιώνα. Αυτό τους επέτρεψε να καθορίσουν πώς μεταβάλλονταν ο λόγος, των τιμών του Bohr, προς τις τιμές που λαμβάνονται με την «τροποποιημένη» μεταβολική αρχή, καθώς ελάμβαναν υπόψη όλο και υψηλότερα ενεργειακά επίπεδα. Ήταν έκπληξη που είδαν ότι ο λόγος απέδωσε αποτελεσματικά τον τύπο του Wallis για το π.
Συγκεκριμένα, ο υπολογισμός των Friedmann και Hagen κατέληξε σε μια έκφραση που περιλαμβάνει ειδικές μαθηματικές συναρτήσεις-ονομάζονται συναρτήσεις γάμμα-που οδηγούν στον τύπο:
ο οποίος μπορεί να αναχθεί στον κλασικό τύπο του Wallis:
Ο μαθηματικός Moshe Machover του King’s College του Λονδίνου αποκαλεί το εύρημα ένα «πονηρό κομμάτι μαγείας». «Αυτή η παραγωγή του π είναι μια έκπληξη του οικείου, μοιάζει σαν ένα κόλπο μάγου», δήλωσε ο Machover. «Ένα παιδί που βλέπει ένα κόλπο να γίνεται για πρώτη φορά μπορεί μόνο να εκπλαγεί. Αλλά ένας ενήλικας, ο οποίος έχει δει πολλά κόλπα με τα χρόνια, βιώνει και έκπληξη και οικειότητα».
Αντιμετωπίζοντας το χάσμα αιώνων μεταξύ του τύπου του Wallis, του 17ου αιώνα, την κβαντική θεωρία του εικοστού αιώνα και τις δεκαετίες που πέρασαν από τότε μέχρι τώρα, ο Doug Ravenel, καθηγητής μαθηματικών στο Πανεπιστήμιο του Rochester, επισημαίνει ότι η Friedmann και ο Hagen χρησιμοποίησαν από παλιά εδραιωμένες έννοιες των πεδίων τους για να καταλήξουν στο αποτέλεσμά τους, έτσι ώστε ακόμη και μαθηματικοί και φυσικοί που έζησαν πριν από πολλές δεκαετίες, θα ήταν σε θέση να το εκτιμήσουν.
«Είναι μια όμορφη σύνδεση μεταξύ του π και της κβαντικής μηχανικής που θα μπορούσε να έχει βρεθεί πριν από 80 χρόνια, αλλά δεν είχε ανακαλυφθεί μέχρι τώρα», δήλωσε ο Ravenel, συγχαίροντας τους δύο συγγραφείς.
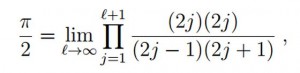
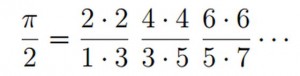
Δεν υπάρχουν σχόλια :
Δημοσίευση σχολίου