Οι ερευνητές υπολόγισαν τον «ένατο αριθμό Dedekind», ο οποίος ανήκει σε μια εκθετικά σύνθετη σειρά αριθμών που ορίζουν εξόδους λογικών συναρτήσεων με βάση διαφορετικές χωρικές διαστάσεις.
Μαθηματικοί οπλισμένοι με υπερυπολογιστές εντόπισαν επιτέλους την αξία ενός μεγάλου αριθμού που προηγουμένως θεωρούνταν αδύνατο να υπολογιστεί.
Ο αριθμός, γνωστός ως “ένατος αριθμός Dedekind” ή D(9), είναι στην πραγματικότητα ο 10ος σε μια ακολουθία. Κάθε αριθμός Dedekind αντιπροσωπεύει τον αριθμό των πιθανών διαμορφώσεων ενός συγκεκριμένου είδους λογικής πράξης true-false σε διαφορετικές χωρικές διαστάσεις.
(Ο πρώτος αριθμός στην ακολουθία είναι D(0), που αντιπροσωπεύει μηδενικές διαστάσεις. Γι’ αυτό το D(9), που αντιπροσωπεύει εννέα διαστάσεις, είναι ο 10ος αριθμός στην ακολουθία.)
Οι αριθμοί Dedekind γίνονται ολοένα και μεγαλύτεροι για κάθε νέα διάσταση, γεγονός που καθιστά όλο και πιο δύσκολο τον προσδιορισμό τους.
Ο όγδοος αριθμός Dedekind, ο οποίος ακολουθεί τους ίδιους κανόνες για οκτώ διαστάσεις, υπολογίστηκε το 1991. Αλλά λόγω του άλματος στην υπολογιστική ισχύ που απαιτείται για τον υπολογισμό της ένατης, ορισμένοι μαθηματικοί θεώρησαν ότι ήταν αδύνατο να υπολογίσουν την ακριβή τιμή του.
Αλλά τώρα, δύο άσχετες μελέτες από ξεχωριστές ερευνητικές ομάδες – η πρώτη που υποβλήθηκε στον διακομιστή προεκτύπωσης arXiv στις 5 Απριλίου και η δεύτερη στον ίδιο διακομιστή στις 6 Απριλίου – έχουν κάνει το αδύνατο. Οι μελέτες -η καθεμία χρησιμοποιώντας έναν υπερυπολογιστή αλλά εκτελούσε διαφορετικά προγράμματα- παρήγαγαν τον ίδιο ακριβώς αριθμό.
Τα αποτελέσματα δεν έχουν ακόμη αξιολογηθεί από ομοτίμους. Αλλά επειδή οι μελέτες κατέληξαν στο ίδιο συμπέρασμα, είναι «100% βέβαιο» ότι ο αριθμός έχει αποκρυπτογραφηθεί σωστά, ο κύριος συγγραφέας στη δεύτερη εργασία, Lennart Van Hirtum, μαθηματικός στο Πανεπιστήμιο Paderborn στη Γερμανία και κύριος συγγραφέας στη δεύτερη εργασία, είπε στο Live Science.
Ο Van Hirtum και οι συνεργάτες του υπερασπίστηκαν το έργο τους κατά τη διάρκεια μιας διάλεξης στο Πανεπιστήμιο Paderborn στις 27 Ιουνίου.
Τι είναι οι αριθμοί Dedekind;
Οι αριθμοί Dedekind περιγράφηκαν για πρώτη φορά από τον Γερμανό μαθηματικό Richard Dedekind τον 19ο αιώνα. Οι αριθμοί σχετίζονται με λογικά προβλήματα γνωστά ως “μονότονες δυαδικές συναρτήσεις” (MBFs).
Οι συναρτήσεις Boolean είναι ένα είδος λογικής που μπορεί να λάβει ως είσοδο μόνο μία από τις δύο τιμές -0 (false) και 1 (true)- και να ξεχωρίσει μόνο αυτές τις δύο τιμές.
Στα MBF μπορείτε να αλλάξετε το 0 με ένα 1 στην είσοδο, αλλά μόνο εάν επιτρέπει στην έξοδο να αλλάξει από 0 σε 1, όχι από 1 σε 0.
Οι αριθμοί Dedekind είναι η έξοδος των MBF όπου η είσοδος είναι συγκεκριμένη χωρική διάσταση.
Αυτή η έννοια μπορεί να προκαλέσει σύγχυση για τους μη μαθηματικούς. Αλλά είναι δυνατό να οπτικοποιήσουμε τι συμβαίνει χρησιμοποιώντας σχήματα για να αναπαραστήσουμε τους αριθμούς Dedekind για κάθε διάσταση, εξήγησε ο Van Hirtum.
Για παράδειγμα, στη δεύτερη διάσταση, ο αριθμός Dedekind σχετίζεται με ένα τετράγωνο, ενώ ο τρίτος μπορεί να αναπαρασταθεί με έναν κύβο, ο τέταρτος και μεγαλύτερος με υπερκύβους.
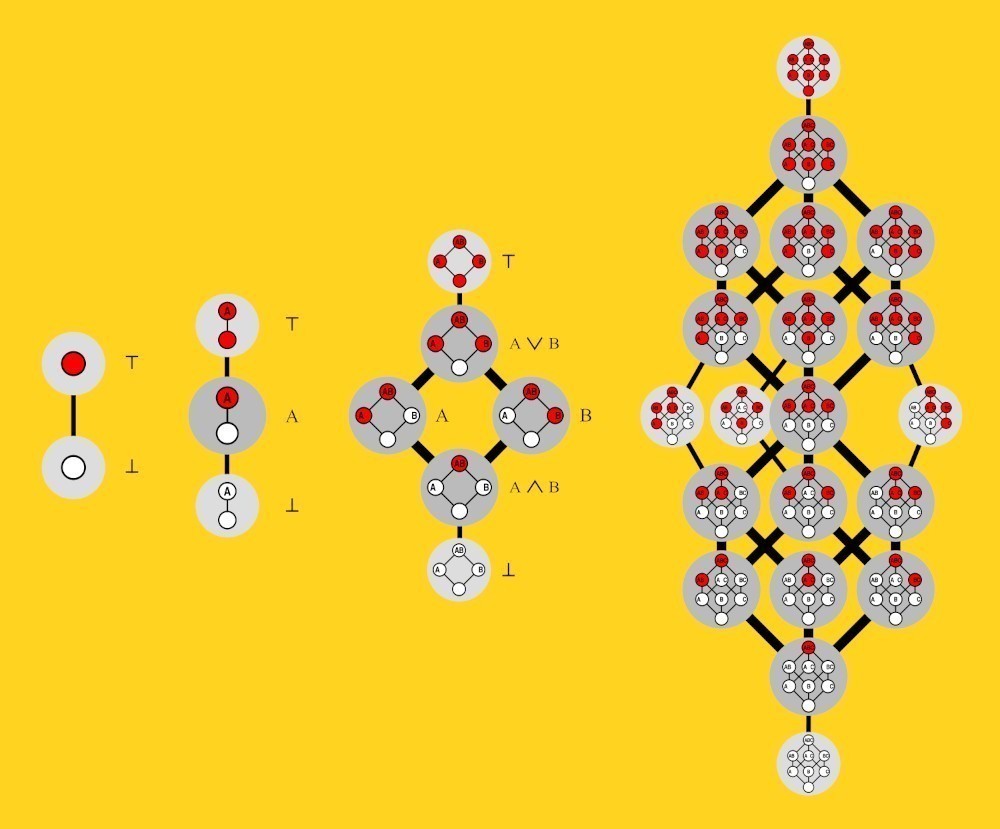
Για κάθε διάσταση, οι κορυφές ή τα σημεία ενός συγκεκριμένου σχήματος αντιπροσωπεύουν τις πιθανές διαμορφώσεις των MBF (βλ. εικόνα).
Για να βρείτε τον αριθμό Dedekind, μπορείτε να μετρήσετε πόσες φορές μπορείτε να χρωματίσετε κάθε κορυφή από κάθε σχήμα με ένα από τα δύο χρώματα (σε αυτήν την περίπτωση κόκκινο και λευκό), αλλά με την προϋπόθεση ότι δεν μπορεί να τοποθετηθεί ένα χρώμα (σε αυτήν την περίπτωση το λευκό). πάνω από το άλλο (σε αυτή την περίπτωση κόκκινο).
Για μηδενικές διαστάσεις, το σχήμα είναι μόνο ένα σημείο και D(0)=2 επειδή το σημείο μπορεί να είναι είτε κόκκινο είτε λευκό. Για μια διάσταση, το σχήμα είναι μια γραμμή με δύο σημεία και D(1)=3 επειδή και τα δύο σημεία μπορεί να είναι είτε το ίδιο χρώμα είτε κόκκινα πάνω από το λευκό.
Για δύο διαστάσεις, το σχήμα είναι τετράγωνο και D(2)=6 επειδή υπάρχουν πλέον έξι πιθανά σενάρια όπου καμία λευκή κουκκίδα δεν βρίσκεται πάνω από μια κόκκινη κουκκίδα. Και για τις τρεις διαστάσεις, το σχήμα είναι ένας κύβος, και ο αριθμός των πιθανών διαμορφώσεων μεταβαίνει σε 20, άρα D(3)=20.
Καθώς ο αριθμός των διαστάσεων αυξάνεται, το υποθετικό σχήμα γίνεται ένας όλο και πιο πολύπλοκος υπερκύβος με μεγαλύτερο αριθμό αποτελεσμάτων, είπε ο Van Hirtum.
Οι τιμές των επόμενων πέντε αριθμών Dedekind είναι 68, 7581, 7828354, 2414682040998 και 56130437228687557907788.
Η τιμή που προσδιορίστηκε πρόσφατα για το D(9) είναι: 286386577668298411128469151667598498812366.
Όλο και πιο περίπλοκοι υπολογισμοί
Ο Van Hirtum εργάζεται για τον εντοπισμό του D(9) για περισσότερα από τρία χρόνια. Για να το κάνει αυτό, δημιούργησε ένα νέο είδος προγράμματος υπολογιστή για να επιτρέψει σε έναν υπερυπολογιστή να επεξεργάζεται τα δεδομένα με συγκεκριμένο τρόπο.
Εάν είχε χρησιμοποιήσει ένα πιο βασικό πρόγραμμα, θα μπορούσαν να χρειαστούν έως και 100 χρόνια για να ολοκληρωθούν οι υπολογισμοί, ακόμη και με ένα προηγμένο μηχάνημα που τσακίζει τους αριθμούς, είπε.
Αφού δημιούργησε τον κώδικα του υπολογιστή του, η ομάδα του Van Hirtum πέρασε περισσότερους από τέσσερις μήνες χρησιμοποιώντας τον υπερυπολογιστή στο Πανεπιστήμιο του Leuven στο Βέλγιο για να επεξεργαστεί τα δεδομένα.
Ωστόσο, οι υπολογισμοί δεν άργησαν πραγματικά να ολοκληρωθούν: Η φύση του προγράμματος σήμαινε ότι ήταν επιρρεπής σε λάθη εν μέρει, πράγμα που σήμαινε ότι η ομάδα έπρεπε να επανεκκινεί συνεχώς την εργασία, είπε ο Van Hirtum.
Συγκριτικά, ο υπολογιστής που χρησιμοποιήθηκε το 1991 για την επεξεργασία του D(8) ήταν λιγότερο ισχυρός από ένα σύγχρονο smartphone και ολοκλήρωσε την εργασία σε περίπου 200 ώρες. Ένας σύγχρονος φορητός υπολογιστής θα μπορούσε πιθανώς να εκτελέσει αυτούς τους υπολογισμούς σε λιγότερο από 10 λεπτά, είπε ο Van Hirtum.
Ο Van Hirtum πιστεύει ότι ένα παρόμοιο άλμα στην επεξεργαστική ισχύ του υπολογιστή θα απαιτηθεί για τον υπολογισμό του 10ου αριθμού Dedekind. «Αν το κάναμε τώρα, θα απαιτούσε επεξεργαστική ισχύ ίση με τη συνολική ισχύ εξόδου του ήλιου», είπε, γεγονός που καθιστά «πρακτικά αδύνατο» τον υπολογισμό.
Οι απαιτήσεις επεξεργαστικής ισχύος θα μπορούσαν να μειωθούν χρησιμοποιώντας πιο σύνθετους αλγόριθμους, είπε ο Van Hirtum.
«Αλλά έχουμε κάπως χτυπήσει έναν τοίχο με το πόσο πολύπλοκοι μπορούν να γίνουν οι αλγόριθμοι», πρόσθεσε.
Ωστόσο, άλλοι μαθηματικοί εξακολουθούν να ελπίζουν ότι το D(10) θα μπορούσε τελικά να υπολογιστεί, είπε ο Van Hirtum.
Δεν υπάρχουν σχόλια :
Δημοσίευση σχολίου