Η ΧΡΥΣΗ ΤΟΜΗ: Το μεγαλύτερο μυστικό της φύσης
Δεν είναι εύκολο να ξετυλίξουμε την ιστορία της χρυσής τομής. Αν και χρησιμοποιήθηκε στην αρχαία Αίγυπτο αλλά και στην πυθαγόρεια παράδοση, ο πρώτος ορισμός που έχουμε γι’ αυτήν ανήκει στον Ευκλείδη (325-265 π.Χ.), που την ορίζει ως διαίρεση ενός ευθύγραμμου τμήματος σε άκρο και μέσο λόγο. Η παλαιότερη γνωστή μελέτη είναι η Θεία αναλογία, έργο του μεθυσμένου από την ομορφιά μοναχού Λούκα Πατσιόλι (1445-1517) που εικονογραφήθηκε από τον Λεονάρντο Ντα Βίντσι, ο οποίος σύμφωνα με την παράδοση επινόησε και τον όρο section aurea δηλαδή «χρυσή τομή». Ωστόσο, η πρώτη δημοσιευμένη χρήση της φράσης βρίσκεται στο έργο Die Reine Elementar-Mathematik [Καθαρά στοιχειώδη μαθηματικά] του Μάρτιν Ομ (1835).
Υπάρχουν πολλά ονόματα για τη μυστηριώδη τομή. Αναφέρεται ως χρυσός ή θείος λόγος, μέσος, αναλογία, αριθμός ή τομή. Στα μαθηματικά συμβολίζεται με το γράμμα τ, που δηλώνει την τομή, ή συχνότερα με το Φ ή το φ, το πρώτο γράμμα από το όνομα του γλύπτη Φειδία, που τη χρησιμοποίησε στον Παρθενώνα.
Τι είναι λοιπόν αυτή η αινιγματική τομή και πού οφείλεται η γοητεία της; Ένα από τα αιώνια ερωτήματα που απασχόλησαν τους φιλοσόφους αφορά το πώς το Ένα γίνεται Πολλά. Ποια η φύση του χωρισμού ή της διαίρεσης; Υπάρχει τρόπος να διατηρήσουν τα μέρη ουσιαστική σχέση με το σύνολο;
Θέτοντας το ερώτημα με αλληγορικούς όρους, ο Πλάτωνας (427-347 π.Χ.) στην Πολιτεία ζητάει από τον αναγνώστη να πάρει μια γραμμή και να τη διαιρέσει άνισα. Καθώς δεσμευόταν από τον πυθαγόρειο όρκο να μην αποκαλύψει τα μυστικά των μυστηρίων, ο Πλάτωνας έθετε ερωτήσεις ελπίζοντας να προκαλέσει μια διορατική απάντηση. Γιατί λοιπόν χρησιμοποιεί μια γραμμή αντί για αριθμούς; Και γιατί μας ζητάει να τη διαιρέσουμε άνισα;
Για να ανταποκριθούμε στην πρόσκλησή του θα πρέπει να κατανοήσουμε το λόγο και την αναλογία.
Ο λόγος είναι η σχέση ενός αριθμού προς έναν άλλο, για παράδειγμα 4:8 («4 προς 8»). Η αναλογία είναι ένας επαναλαμβανόμενος λόγος που συνήθως περιλαμβάνει τέσσερις όρους, όπως 4:8 :: 5:10 («το 4 προς 8 είναι ό,τι το 5 προς 10»). Οι Πυθαγόρειοι την αποκαλούσαν ασυνεχή αναλογία τεσσάρων όρων. Ο σταθερός λόγος εδώ είναι το 1:2, που επαναλαμβάνεται στο 4:8 και στο 5:10. Ο ανεστραμμένος λόγος αντιστρέφει τους όρους, έτσι το 8:4 είναι το αντίστροφο του 4:8 και ο σταθερός λόγος είναι τώρα 2:1. Μεταξύ του λόγου δύο όρων και της αναλογίας τεσσάρων όρων βρίσκεται ο μέσος τριών όρων, στον οποίο ο μεσαίος όρος διαθέτει τον ίδιο λόγο με τον πρώτο που έχει ο τελευταίος με τον ίδιο. Ο γεωμετρικός μέσος δύο αριθμών ισούται με την τετραγωνική ρίζα του γινομένου τους. Έτσι, ο γεωμετρικός μέσος π.χ. του 1 και του 9 είναι √(1Χ9)=3. Η σχέση αυτή γράφεται 1:3:9 ή, ανεστραμμένη, 9:3:1. Μπορεί επίσης να γραφτεί πληρέστερα ως συνεχής γεωμετρική αναλογία, όπου οι δύο αυτοί λόγοι επαναλαμβάνουν τον ίδιο σταθερό λόγο 1:3. Δηλαδή, 1:3 :: 3:9. Το 3 είναι ο γεωμετρικός μέσος που είναι κοινός για τους δύο λόγους, συνδέοντας ή διαπλέκοντάς τους σε αυτό που οι Πυθαγόρειοι αποκαλούσαν συνεχή γεωμετρική αναλογία τριών όρων.
Ο Πλάτωνας θεωρεί ότι η συνεχής γεωμετρική αναλογία αποτελεί τον βαθύτερο κοσμικό δεσμό. Στον Τίμαιο, η ψυχή του κόσμου συγκροτείται σε αρμονική συνήχηση, αποτελούμενη στο πάνω μέρος από τον νοητό κόσμο των μορφών (συμπεριλαμβανομένων των καθαρών μαθηματικών) και στο κάτω από τον ορατό κόσμο των υλικών αντικειμένων, μέσω των ακολουθιών 1, 2, 4, 8 και 1, 3, 9, 27.
Για να επιστρέψουμε λοιπόν στο γρίφο μας, ας αναρωτηθούμε γιατί μας ζητάει ο Πλάτωνας να κάνουμε ασύμμετρη τομή; Μια συμμετρική τομή θα έδινε λόγο συνόλου προς τμήμα 2:1 και λόγο των δύο ίσων τμημάτων 1:1. Οι λόγοι αυτοί δεν ισούνται κι έτσι δεν παρουσιάζεται αναλογία.
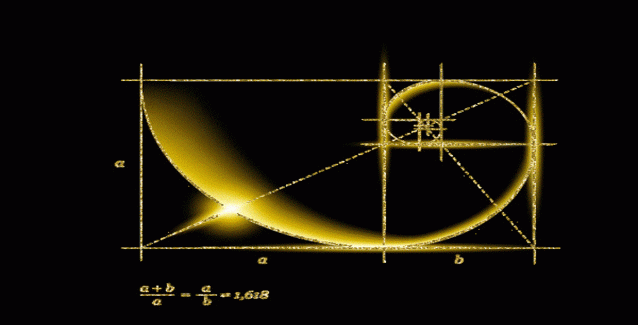
Υπάρχει μόνο ένας τρόπος να σχηματίσουμε αναλογία από έναν απλό λόγο, κι αυτός είναι η χρυσή τομή. Ο Πλάτωνας θέλει να ανακαλύψουμε έναν ιδιαίτερο λόγο, τέτοιον ώστε το σύνολο προς το μεγαλύτερο τμήμα να ισούται με το μεγαλύτερο τμήμα προς το μικρότερο. Γνωρίζει ότι αυτό θα μας οδηγούσε στον προσφιλή του στη φύση δεσμό, μια συνεχή γεωμετρική αναλογία. Το αντίστροφο ισχύει επίσης, ο λόγος του μικρότερου τμήματος προς το μεγαλύτερο ισούται με το λόγο του μεγαλύτερου προς το σύνολο.
Γιατί όμως χρησιμοποιεί ένα ευθύγραμμο τμήμα και όχι απλώς αριθμούς; Ο Πλάτωνας γνώριζε ότι η απάντηση είναι ένας άρρητος αριθμός, που μπορούμε να προσδιορίσουμε γεωμετρικά σ’ ένα ευθύγραμμο τμήμα αλλά δεν μπορεί να εκφραστεί ως απλό κλάσμα.
Αν λύσουμε το πρόβλημα μαθηματικά, και υποθέτοντας ότι ο μέσος (μεγαλύτερο τμήμα) έχει μήκος 1, βρίσκουμε μεγάλη χρυσή τιμή 1,6180399… (για το σύνολο) και μικρή χρυσή τιμή 0,6180399… (για το μικρότερο τμήμα). Ορίζουμε αυτά Φ για το μεγάλο και φ για το μικρό, αντίστοιχα. Σημειώνουμε ότι τόσο το γινόμενό τους όσο και η διαφορά τους δίνουν τη μονάδα. Επιπλέον, το τετράγωνο του Φ είναι 2,6180399, ή Φ+1. Κι ακόμη, το καθένα είναι αντίστροφο του άλλου, δηλαδή το φ ισούται με 1/Φ.
Δεν είναι εύκολο να ξετυλίξουμε την ιστορία της χρυσής τομής. Αν και χρησιμοποιήθηκε στην αρχαία Αίγυπτο αλλά και στην πυθαγόρεια παράδοση, ο πρώτος ορισμός που έχουμε γι’ αυτήν ανήκει στον Ευκλείδη (325-265 π.Χ.), που την ορίζει ως διαίρεση ενός ευθύγραμμου τμήματος σε άκρο και μέσο λόγο. Η παλαιότερη γνωστή μελέτη είναι η Θεία αναλογία, έργο του μεθυσμένου από την ομορφιά μοναχού Λούκα Πατσιόλι (1445-1517) που εικονογραφήθηκε από τον Λεονάρντο Ντα Βίντσι, ο οποίος σύμφωνα με την παράδοση επινόησε και τον όρο section aurea δηλαδή «χρυσή τομή». Ωστόσο, η πρώτη δημοσιευμένη χρήση της φράσης βρίσκεται στο έργο Die Reine Elementar-Mathematik [Καθαρά στοιχειώδη μαθηματικά] του Μάρτιν Ομ (1835).
Υπάρχουν πολλά ονόματα για τη μυστηριώδη τομή. Αναφέρεται ως χρυσός ή θείος λόγος, μέσος, αναλογία, αριθμός ή τομή. Στα μαθηματικά συμβολίζεται με το γράμμα τ, που δηλώνει την τομή, ή συχνότερα με το Φ ή το φ, το πρώτο γράμμα από το όνομα του γλύπτη Φειδία, που τη χρησιμοποίησε στον Παρθενώνα.
Τι είναι λοιπόν αυτή η αινιγματική τομή και πού οφείλεται η γοητεία της; Ένα από τα αιώνια ερωτήματα που απασχόλησαν τους φιλοσόφους αφορά το πώς το Ένα γίνεται Πολλά. Ποια η φύση του χωρισμού ή της διαίρεσης; Υπάρχει τρόπος να διατηρήσουν τα μέρη ουσιαστική σχέση με το σύνολο;
Θέτοντας το ερώτημα με αλληγορικούς όρους, ο Πλάτωνας (427-347 π.Χ.) στην Πολιτεία ζητάει από τον αναγνώστη να πάρει μια γραμμή και να τη διαιρέσει άνισα. Καθώς δεσμευόταν από τον πυθαγόρειο όρκο να μην αποκαλύψει τα μυστικά των μυστηρίων, ο Πλάτωνας έθετε ερωτήσεις ελπίζοντας να προκαλέσει μια διορατική απάντηση. Γιατί λοιπόν χρησιμοποιεί μια γραμμή αντί για αριθμούς; Και γιατί μας ζητάει να τη διαιρέσουμε άνισα;
Για να ανταποκριθούμε στην πρόσκλησή του θα πρέπει να κατανοήσουμε το λόγο και την αναλογία.
Ο λόγος είναι η σχέση ενός αριθμού προς έναν άλλο, για παράδειγμα 4:8 («4 προς 8»). Η αναλογία είναι ένας επαναλαμβανόμενος λόγος που συνήθως περιλαμβάνει τέσσερις όρους, όπως 4:8 :: 5:10 («το 4 προς 8 είναι ό,τι το 5 προς 10»). Οι Πυθαγόρειοι την αποκαλούσαν ασυνεχή αναλογία τεσσάρων όρων. Ο σταθερός λόγος εδώ είναι το 1:2, που επαναλαμβάνεται στο 4:8 και στο 5:10. Ο ανεστραμμένος λόγος αντιστρέφει τους όρους, έτσι το 8:4 είναι το αντίστροφο του 4:8 και ο σταθερός λόγος είναι τώρα 2:1. Μεταξύ του λόγου δύο όρων και της αναλογίας τεσσάρων όρων βρίσκεται ο μέσος τριών όρων, στον οποίο ο μεσαίος όρος διαθέτει τον ίδιο λόγο με τον πρώτο που έχει ο τελευταίος με τον ίδιο. Ο γεωμετρικός μέσος δύο αριθμών ισούται με την τετραγωνική ρίζα του γινομένου τους. Έτσι, ο γεωμετρικός μέσος π.χ. του 1 και του 9 είναι √(1Χ9)=3. Η σχέση αυτή γράφεται 1:3:9 ή, ανεστραμμένη, 9:3:1. Μπορεί επίσης να γραφτεί πληρέστερα ως συνεχής γεωμετρική αναλογία, όπου οι δύο αυτοί λόγοι επαναλαμβάνουν τον ίδιο σταθερό λόγο 1:3. Δηλαδή, 1:3 :: 3:9. Το 3 είναι ο γεωμετρικός μέσος που είναι κοινός για τους δύο λόγους, συνδέοντας ή διαπλέκοντάς τους σε αυτό που οι Πυθαγόρειοι αποκαλούσαν συνεχή γεωμετρική αναλογία τριών όρων.
Ο Πλάτωνας θεωρεί ότι η συνεχής γεωμετρική αναλογία αποτελεί τον βαθύτερο κοσμικό δεσμό. Στον Τίμαιο, η ψυχή του κόσμου συγκροτείται σε αρμονική συνήχηση, αποτελούμενη στο πάνω μέρος από τον νοητό κόσμο των μορφών (συμπεριλαμβανομένων των καθαρών μαθηματικών) και στο κάτω από τον ορατό κόσμο των υλικών αντικειμένων, μέσω των ακολουθιών 1, 2, 4, 8 και 1, 3, 9, 27.
Για να επιστρέψουμε λοιπόν στο γρίφο μας, ας αναρωτηθούμε γιατί μας ζητάει ο Πλάτωνας να κάνουμε ασύμμετρη τομή; Μια συμμετρική τομή θα έδινε λόγο συνόλου προς τμήμα 2:1 και λόγο των δύο ίσων τμημάτων 1:1. Οι λόγοι αυτοί δεν ισούνται κι έτσι δεν παρουσιάζεται αναλογία.
Υπάρχει μόνο ένας τρόπος να σχηματίσουμε αναλογία από έναν απλό λόγο, κι αυτός είναι η χρυσή τομή. Ο Πλάτωνας θέλει να ανακαλύψουμε έναν ιδιαίτερο λόγο, τέτοιον ώστε το σύνολο προς το μεγαλύτερο τμήμα να ισούται με το μεγαλύτερο τμήμα προς το μικρότερο. Γνωρίζει ότι αυτό θα μας οδηγούσε στον προσφιλή του στη φύση δεσμό, μια συνεχή γεωμετρική αναλογία. Το αντίστροφο ισχύει επίσης, ο λόγος του μικρότερου τμήματος προς το μεγαλύτερο ισούται με το λόγο του μεγαλύτερου προς το σύνολο.
Γιατί όμως χρησιμοποιεί ένα ευθύγραμμο τμήμα και όχι απλώς αριθμούς; Ο Πλάτωνας γνώριζε ότι η απάντηση είναι ένας άρρητος αριθμός, που μπορούμε να προσδιορίσουμε γεωμετρικά σ’ ένα ευθύγραμμο τμήμα αλλά δεν μπορεί να εκφραστεί ως απλό κλάσμα.
Αν λύσουμε το πρόβλημα μαθηματικά, και υποθέτοντας ότι ο μέσος (μεγαλύτερο τμήμα) έχει μήκος 1, βρίσκουμε μεγάλη χρυσή τιμή 1,6180399… (για το σύνολο) και μικρή χρυσή τιμή 0,6180399… (για το μικρότερο τμήμα). Ορίζουμε αυτά Φ για το μεγάλο και φ για το μικρό, αντίστοιχα. Σημειώνουμε ότι τόσο το γινόμενό τους όσο και η διαφορά τους δίνουν τη μονάδα. Επιπλέον, το τετράγωνο του Φ είναι 2,6180399, ή Φ+1. Κι ακόμη, το καθένα είναι αντίστροφο του άλλου, δηλαδή το φ ισούται με 1/Φ.
Δεν υπάρχουν σχόλια :
Δημοσίευση σχολίου